데이터 사이언티스트에게 ‘선형대수’ 지식이 왜 필요할까?
선형대수란, 벡터공간, 벡터, 선형결합, 행렬, 연립선형방정식 등을 연구하는 대수학의 한 분야입니다.
데이터분석을 하게되면 하나의 관측치에 대하여 여러 특성을 가지고 있는 경우가 많습니다. 분석값에 대한 결과로 target을 찾게 될때 이 여러 특성이 관여하는 가중치를 계산하는데, 수식으로 나타내면 다음과 같습니다.
예시: '연봉'이라는 target을 찾기 위해 '교육', '경력', '인종', '성별' 등 다양한 특성이 있다고 해보겠습니다.
그럼 다음과 같은 표현이 가능합니다.
연봉 = (0.7) * 교육 + (0.3) * 경력 + 1.2 * 인종 + 0.5 * 성별
당연히 앞의 가중치는 다를 것입니다.
이런 식으로 가중치, 특성값이 변하면서 연봉을 구할 수 있게 됩니다. 다시 한번 열벡터와 행벡터로 표현해보면 다음과 같습니다.
\begin{align}
\vec{weight} =
\begin{bmatrix}
0.7 & 0.3 & 1.2 & 0.5
\end{bmatrix}
\qquad
\vec{feature} =
\begin{bmatrix}
교육
경력
인종
성별
\end{bmatrix}
\qquad
연봉 = \vec{weight} * \vec{feature}
\end{align}
또한 각 관측치에 따라 특성들이 관찰되었다면, 연립방정식을 풀어야하고 이를 행렬로 나타내어 해결할 수 있습니다.
이처럼 벡터, 행렬 등 n차원의 정보를 다루기 위해서는 선형대수가 필요하고, 우리는 데이터들을 n차원 공간위의 데이터로 인식하여 계산할 필요가 있습니다.
스칼라, 벡터, 행렬, 텐서
스칼라와 벡터는 선형 대수를 구성하는 기본 단위입니다. 스칼라는 ‘크기’, 벡터는 ‘크기’와 ‘방향’을 가집니다.
직선 방정식은 행렬과 벡터로 풀어 쓸 수 있습니다.
스칼라
단일 숫자이며, 변수에 저장 할때는 일반적으로 소문자를 이용하여 표기합니다. 스칼라는 실수와 정수 모두 가능합니다.
\begin{align} a = 4 \qquad b = 4.7 \qquad c = 1.2\mathrm{e}{+2} \qquad d = \pi \end{align}
벡터
스칼라를 한 방향으로 정렬한 것으로, 벡터를 구성하는 스칼라값들을 요소나 성분이라고 합니다.
$\vec{a}$는 해당 요소를 수직 방향으로 늘어놓은 열 벡터, $\vec{b}$는 해당 요소를 수평 방향으로 늘어놓은 행 벡터라고 합니다.
\begin{align}
\vec{a} =
\begin{bmatrix}
a_{1}
a_{2}
a_{3}
\end{bmatrix}
\qquad
\vec{b} =
\begin{bmatrix}
b1 & b2 & b3
\end{bmatrix}
\qquad
\end{align}
행렬
같은 크기의 벡터를 복수로 늘어놓은 것입니다.
\begin{align}
A =
\begin{bmatrix}
a_{1,1} & a_{1,2} & a_{1,3}
a_{2,1} & a_{2,2} & a_{2,3}
a_{3,1} & a_{3,2} & a_{3,3}
\end{bmatrix}
\end{align}
텐서
텐서(tensor)는 벡터나 행렬을 일반화한 개념입니다. 벡터는 1차원 텐서이고 행렬은 2차원 텐서로 나타낼 수 있습니다.
이 개념을 더욱 발전시켜 행렬을 더욱 늘어놓은 것을 3차원 텐서라고 합니다. 그 이상 차원도 텐서로 표현이 가능하며,보통 ‘텐서’라 하면 3차원 이상의 텐서를 의미합니다.
벡터의 연산 및 행렬의 연산, 행렬의 속성
벡터의 연산
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print("벡터덧셈:\n", a + b)
print("벡터뺼셈:\n", a - b)
print("벡터내적stpe1:\n", a*b)
print("백터내적step2:\n", (a*b).sum())
print("벡터내적_np함수:\n", np.dot(a,b))
벡터덧셈:
[5 7 9]
벡터뺼셈:
[-3 -3 -3]
벡터내적stpe1:
[ 4 10 18]
백터내적step2:
32
벡터내적_np함수:
32
행렬의 연산
행과 열의 크기가 같은 행렬끼리만 연산이 가능하고, 덧셈과 뺄셈, 요소끼리 곱이 벡터와 동일합니다.
#np에서는 2차원배열로 나타냄
A = np.array([[1,2], [4,5]])
B = np.array([[3,4], [7,8]])
print("행렬덧셈:\n", A + B)
print("행렬뺼셈:\n", A - B)
print("행렬 같은위치요소 곱:\n", A*B)
# print("백터내적step2:", (a*b).sum())
# print("벡터내적_np함수:", np.dot(a,b))
행렬덧셈:
[[ 4 6]
[11 13]]
행렬뺼셈:
[[-2 -2]
[-3 -3]]
행렬 같은위치요소 곱:
[[ 3 8]
[28 40]]
행렬의 속성
Dimensionality
매트릭스의 행과 열의 숫자를 차원 (dimension, 차원수등.)이라 표현합니다. 추가로, 차원을 표기 할때는 행을 먼저, 열을 나중에 표기합니다. (행-열)
ex) 3x3 (3 by 3)
일치
2개의 매트릭스가 일치하기 위해서는, 다음 조건을 만족해야 합니다:
- 동일한 차원을 보유.
- 각 해당하는 구성요소들이 동일.
Transpose
매트릭스의 전치는, 행과 열을 바꾸는 것을 의미합니다. 다음과 같이 표기합니다.
\begin{align} B^{T} \qquad B^{\prime} \end{align}
B transpose 혹은 B prime라고 읽습니다. 대각선 부분의 구성요소를 고정시키고 이를 기준으로 나머지 구성요소들을 뒤집는다 라고 생각하면 됩니다.

A = np.array([[1,2], [4,5]])
print("base:\n",A)
print("transpose:\n", A.T)
base:
[[1 2]
[4 5]]
transpose:
[[1 4]
[2 5]]
Determinant
행렬식은 모든 정사각 매트릭스가 갖는 속성으로, $det(A)$ 혹은 $|A|$로 표기 됩니다.
2x2 매트릭스를 기준으로, 행렬식은 다음과 같이 (AD-BC) 계산 할 수 있습니다:
\begin{align}
\qquad
\begin{bmatrix}
8 & 12
9 & 16
\end{bmatrix}
\end{align}
\begin{align} 8 * 16 - 12 * 9 = 20 \end{align}
\begin{align} |x| = det(x) = 20 \end{align}
n = np.array([[8,12],[9,16]])
det = numpy.linalg.det(n)
print(det)
19.999999999999996
Inverse
- 행렬의 역수 와 같이 표현 할 수 있습니다.
- 행렬과 그 역행렬의 값은 항상 I (단위 매트릭스) 입니다. 2x2 매트릭스를 기준으로, 역행렬을 계산하는 방식중 하나는 아래와 같습니다:
\begin{align}
A = \begin{bmatrix}
a & b
c & d
\end{bmatrix}
\qquad
A^{-1} = \frac{1}{ad-bc}\begin{bmatrix}
d & -b
-c & a
\end{bmatrix}
\qquad
AA^{-1}=I
\end{align}
A = np.array([[1,2], [4,5]])
print("base:\n", A)
A_inv = np.linalg.inv(A)
print("inverse:\n", A_inv)
base:
[[1 2]
[4 5]]
inverse:
[[-1.66666667 0.66666667]
[ 1.33333333 -0.33333333]]
공분산과 상관계수
공분산
두 변량(확률변수) 간에 상관성/의존성/유사성의 방향* 및 정도에 대한 척도이며, 두 변량(Variate) 간에 상관관계(Correlation)의 측도(Measure)입니다.
확률변수 X의 평균, Y의 평균을 각각
\begin{align}
E(X) = \mu,
\qquad
E(Y) = \nu
\end{align}
이라 했을 때, X, Y의 공분산은 다음과 같습니다.
\begin{align}
Cov(X, Y) = E((X-\mu)(Y-\nu))
\end{align}
즉. 공분산은 X의 편차, Y의편차를 곱하여 평균을 구한 값입니다.
하지만 공분산은 ‘scale’이 되어있지 않아, 각 변량들의 단위 크기에 영향을 받습니다. 따라서 해결방법으로 등장한 것이 상관계수입니다.
상관계수
상관 계수 (Correlation Coefficient) = 정규화된 공분산
공분산이 각 변량의 단위에 의존하게되어 변동 크기량이 모호하므로, 확률변수의 절대적 크기에 영향받지 않도록, 각 변량의 표준편차의 크기만큼 나누어 단위화를 시켜준 것이다.
Var() : 분산, σX : 표준편차, Cov(X,Y) : 공분산 라 할 때, 상관계수는 다음과 갑습니다.
\begin{align}
cor(X,Y) = \rho = \frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}}
\end{align}
상관계수는 단위가 무차원(dimensionless)이고, 값 범위가 -1 ≤ ρ ≤ 1입니다.
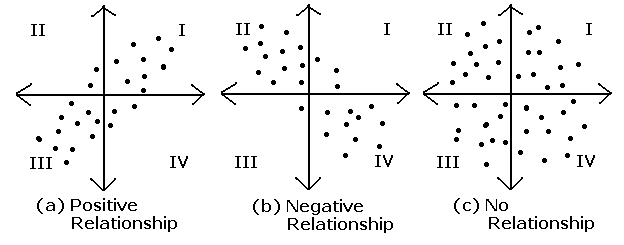
상관계수를 통해 위의 그림을 표현할 수 있는데, (a)의 경우, 두 변량이 양의 상관관계를 가지고 있어 상관계수가 positive, (b)의 경우, 반대로 negative입니다. (c)의 경우 어떠한 상관관계가 보이지 않아 상관계수가 0이라고 할 수 있겠습니다.
데이터분석에서 상관관계 분석을 하는 이유는 데이터간의 유사도를 구하는 것입니다. 상관계수를 활용하여, 두 데이터간의 변화패턴이 일치할수록 두 데이터는 유사한 데이터가 됩니다. 하지만 두 변수가 서로 인과관계를 가진다는 의미는 아닙니다.
선형대수 keyword정리
Orthogonality
수학적으로, 각 요소들이 서로 독립적임을 의미하며, 신호/현상 상호간에 전혀 관련성이 없음을 의미합니다.
Span
Span 이란, 주어진 두 벡터의 (합이나 차와 같은) 조합으로 만들 수 있는 모든 가능한 벡터의 집합입니다.
즉, 벡터 v1, v2, … vn들의 가능한 모든 선형 조합으로 공간을 형성하는 것을 의미합니다.
Basis
벡터들은 바로 어떤 공간을 “span”하면서 그들이 독립(Independent)인 벡터들입니다.
Rank
rank란, 행렬의 열을 이루고 있는 벡터들로 만들 수 있는 (span) 공간의 차원입니다. 즉 행렬이 나타낼 수 있는 벡터 공간에서 기저의 개수입니다. 서로 선형 독립인 벡터가 몇 개가 되는지만 확인하면 됩니다. 차원과는 다를 수도 있으며 그 이유는 행과 열을 이루고 있는 벡터들 가운데 서로 선형 관계가 있을 수도 있기 때문입니다.
Gaussian Elimination
Gaussian Elimination 은 주어진 매트릭스를 “Row-Echelon form”으로 바꾸는 계산과정입니다.
여기서 “Row-Echelon form”이란, 각 행에 대해서 왼쪽에 1, 그 이후 부분은 0으로 이뤄진 형태입니다.
계산과정은 아래 주소에 있습니다.
Reference
https://m.blog.naver.com/sw4r/221942487071
https://lazyis.tistory.com/69?category=726526
https://blog.naver.com/sw4r/221025662499