Thanks for coming

Linear Projection

투영(Projection)이란

사전적 의미: ‘물체의 그림자를 어떤 물체 위에 비추는 일 또는 그 비친 그림자’, ‘도형이나 입체를 다른 평면에 옮기는 일’

선형대수에서의 projection:

vector b를 vector a에 투영시킨 vector p를 다음 표기법으로 나타낼 수 있습니다.

\begin{align} p = proj_{a}(b) \end{align}

original

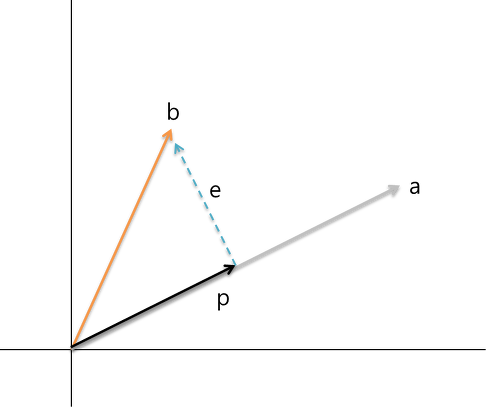
vector p는 vector b를 vector a를 이용하여 나타낼 수 있는 최선의 결과입니다. 완벽하게 vector b를 설명할 수 없지만, 이 최선의 결과가 머신러닝과 딥러닝에 어떻게 적용되는지 살펴보겠습니다.

데이터가 고차원의 데이터일 때, projection을 통해 차원을 축소할 수 있는데, 이를 잘 활용한 방법이 PCA입니다. PCA에 대해서는 아래서 조금 더 자세히 다루겠습니다.
예를 들어 데이터 feature가 각각 x,y로 표현된다면, data를 2차원인 vector (x,y)로 표현할 수 있습니다. 만약 1차원으로 표현하고 싶다면, x축에 투영하는 경우, y축에 투영하는 경우 등이 있습니다. 하지만 이 두 방법은 데이터가 같은 x값을 가지거나, 같은 y값을 갖게되면, 투영한 값이 겹치게 되어 데이터의 유실이 생깁니다.

그렇다면 정보의 유실을 막고, 1차원으로 줄일려면 x축, y축이 아닌 다른 축에 데이터를 모으면 됩니다. 위의 그림처럼 vector a 축에 data들을 투영시켜 vector a로만으로 표현하는 방법이 되겠습니다.

최소자승법(least square method)

투영이라는 개념을 최소자승법과 연관지어 볼 수 있습니다. 다음과 같은 방정식이 있는 경우를 보겠습니다.

2x - 8 = 0
3x - 11 = 0
4x - 15 = 0

첫번째 방정식을 풀게되면 x = 4라는 해를 찾게 되는데, 이 해로 두번째 방정식, 세번째 방정식을 해결할 수 없습니다. 두번째 방정식의 해로도, 세번째 방정식의 해로도 이 3개의 방정식의 해를 찾을 수 없습니다. 실생활에서는 이러한 경우가 상당히 많은데, 이런 경우에서는 완벽한 답을 찾지못하여도, 최선의 답을 구해야 한다.

최선의 답을 a라고 할 때, 완벽한 답은 아니기에 각 방정식은 근소한 에러를 갖게 되는데 위의 방정식은 다음과 같이 바꿀 수 있습니다.

2a - 8 = e1
3a - 11 = e2
4a - 15 = e3

이 에러들의 제곱의 총 합을 E라고 할 때, 최선의 답은 이 E값이 가장 작을 때를 만족시키는 답이 됩니다.

E^2 = (2a - 8)^2 + (3a - 11)^2 + (4a - 15)^2

미분을 통해 최소값을 찾아보면, 다음과 같습니다.
\begin{align} \frac{dE^2} {da} = \frac {d} {da} [(2a - 8)^2 + (3a - 11)^2 + (4a - 15)^2] \end{align}

\begin{align} [2 * 2 * (2a - 8) + 2 * 3 * (3a - 11) + 2 * 4 * (4a - 15)] = 0 \end{align}

\begin{align} [8a - 32) + (18a - 66) + (32a - 120)] = 0 \end{align}

\begin{align} 58a - 218 = 0 \end{align}

\begin{align} a = 3.7586… \end{align}

따라서 투영또한 최소자승법처럼 실제 데이터들이 완벽하게 설명되지 않을 때, 최적의 해를 표현할 수 있는 축을 찾아 투영하여, 차원을 축소한다고 생각할 수 있습니다.

Linear transformation

위키백과 정의: 선형변환은 선형 결합을 보존하는, 두 벡터 공간 사이의 함수이다.
먼저, 선형결합을 보존한다는 뜻을 알아보겠습니다. 선형결합은 다음과 같은 조건을 만족합니다.

\begin{align} T(u+v) = T(u)+T(v) \end{align}

\begin{align} T(cu) = cT(u) \end{align}

하나의 수식으로 합쳐서 쓰면 다음과 같이 표현할 수 있습니다.

\begin{align} T(ku+mv) = kT(u)+mT(v) \end{align}

u, v를 vector 공간을 나타내는 basis vector라고 하고, u와 v 벡터로 표현한 임의의 vector를 변환한 값은, u를 변환한 새로운 basis1, v를 변환한 새로운 basis2를 가지고 나타낸 vector공간에서 스칼라배를 통해 구한 값과 동일하다는 의미를 가집니다.
즉 선형변환은 data를 이 선형결합을 유지하면서 임의의 벡터공간에서 transform함수를 통해 새로운 벡터공간에 new data로 mapping시키는 것을 말하며 연산에 사용되는 함수 T는 행렬로 표현이 가능합니다.

Eigenvector, Eigenvalue

고유벡터란, 벡터의 중요 성질인 방향을 변화하지 않고 오직 크기만 변화하는 벡터를 의미합니다. 즉, 위의 linear transformation은 벡터공간과 축을 변환시켜 벡터의 방향과 크기가 달라지는데, 이 중 transformation에 방향은 영향받지 않고, 크기만 변하게 되는 벡터를 고유벡터라고 합니다.

tranform하는 행렬을 A, 바꾸자 하는 벡터를 v라 할 때, 다음과 같은 수식으로 나타낼 수 있습니다.
\begin{align} Av=\lambda v \quad (\lambda는 \;스칼라값) \end{align} 이 때, v를 Eigenvector, $\lambda$를 Eigenvalue라 합니다.

Curse of Dimensionality

차원의 저주란, 수학적 공간차원(=변수 개수)이 늘어나면서 ,문제 계산법이 지수적으로 커지는 상황입니다.
데이터의 입장에서는 차원이 높아질수록 데이터 사이의 거리가 멀어지고, 빈공간이 증가하는 공간의 성김현상(sparsity)가 나타납니다.
Feature가 많을수록 동일한 데이터를 설명하는 빈공간이 증가하고, 이는 알고리즘 처리과정에서 저장공간과 처리 시간이 불필요하게 증가하여 성능을 저하시킵니다.
일반적으로 머신러닝은 주어진 데이터셋을 통해 학습을 하고 학습된 모델로 예측을 합니다. 이때 데이터가 너무 고차원이라 훈련 데이터셋이 충분히 전체공간을 나타내지 못하고 학습 모델이 특정 부분만 학습하게 되면 과적합(overfitting)이 됩니다. 즉, 데이터가 충분하지 못할 때 고차원으로 표현된 데이터는 과적합을 발생시킵니다.
물론 이에 대해서 정확하게 정해진 기준이 있는 건 아니지만, 일반적으로 feature의 수를 P , sample의 수를 N 이라 할 때 P ≥ N 인 경우 매우 높은 overfitting 이슈가 생긴다고 할 수 있습니다.
이를 해결하기 위해서는 데이터의 수를 충분히 늘리거나, 고차원의 데이터를 차원축소를 통해 저차원의 데이터로 변환을 시켜야 합니다.

차원축소의 방법을 Feacture Selection, Feature Extraction 두 종류로 나눠볼 수 있습니다.

original

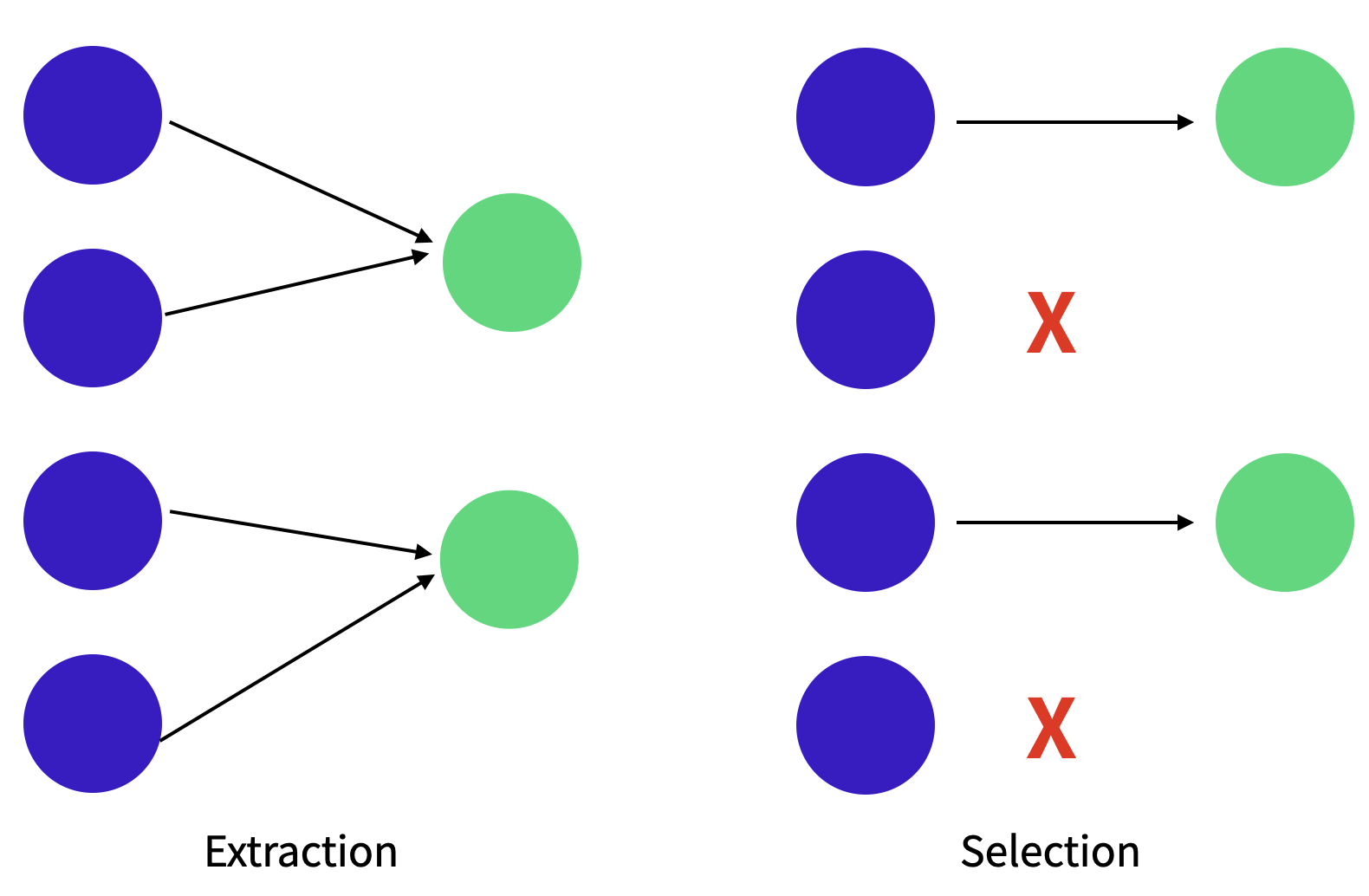
Feature Selection 의 경우, 필요한 Feature만 선택을 하여 해석이 쉬우나, feature들간의 연관성을 살펴봐야 합니다.
Feature extraction의 경우, feature들의 조합으로 새로운 feature를 선택하는 등의 방법으로 feature 들간의 연관성을 고려하여 feature수를 많이 줄일 수 있지만, 조합된 feature에 대해 해석이 어려운 단점이 있습니다.

PCA(Principle component Analysis)

feature extraction의 방법중 하나로, 다차원의 데이터 분포를 가장 잘 표현할 수 있는 성분들 PC들을 찾아 저차원의 data분포로 표현하는 알고리즘입니다.

위에서 설명한 linear projection, linear transformation, Eigenvector, Eigenvalue 개념들을 토대로 PCA를 설명해보도록 하겠습니다.

고차원 data의 특성을 잘 설명할 수 있게 저차원의 새로운 축으로 linear projection을 하는데, data의 유실이 가장 적게 발생할 수 있도록 분산값이 가장 큰 값을 갖는 축을 찾습니다. 이 축을 PC1라고 합니다.

이 PC1를 찾기 위해서는 covariance의 eigen vector값을 찾아야 하고, 이 중 가장 큰 값을 갖는 vector가 PC1가 됩니다.

그리고 PC1에 수직이면서 그 다음 큰 값을 갖는 vector를 PC2라고 하고 그 다음 축들도 연달아 찾아줄 수 있습니다.

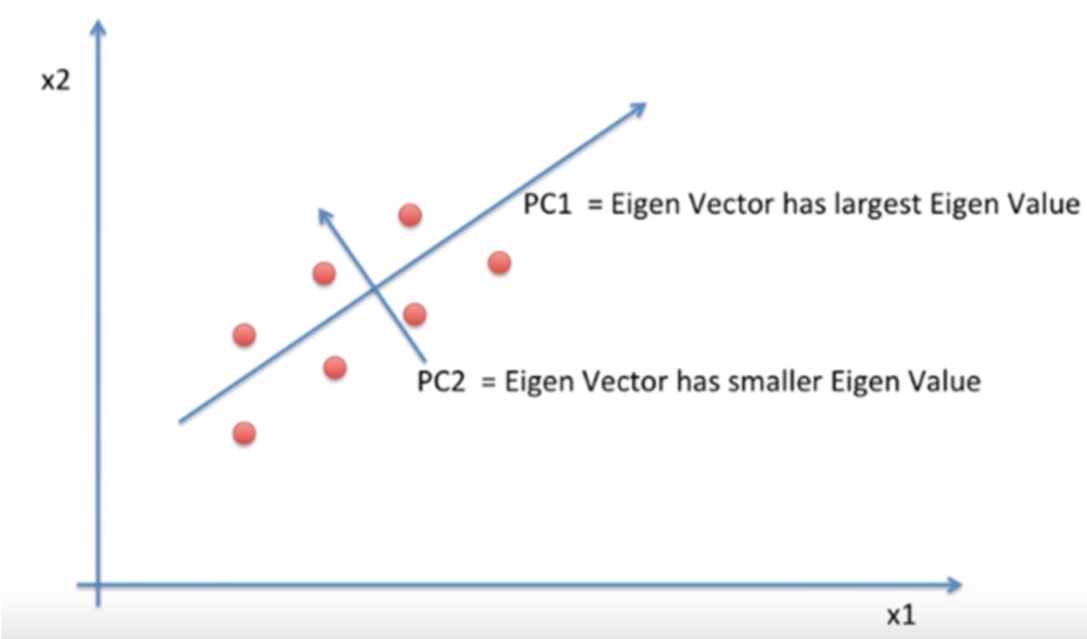
이렇게 찾아준 PC축으로 이루어진 새로운 좌표계에 원래의 data를 linear transformation통해 mapping하여 새로운 data를 찾습니다. 이처럼 PCA는 PC들 중 특징을 나타낼 때 미치는 영향을 분석하여, 미미한 영향을 주는 PC는 삭제하는 등 특징을 가장 잘살리면서 차원을 축소하는 것을 목표로 하고 있습니다.

PCA 실습

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

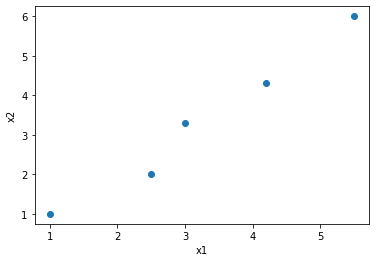
df = pd.DataFrame({"x1": [1, 2.5, 3, 4.2, 5.5] , "x2": [1, 2, 3.3, 4.3, 6]})

threedee = plt.figure().gca()
threedee.scatter(df['x1'], df['x2'])
threedee.set_xlabel('x1')
threedee.set_ylabel('x2')
plt.show()

original

X = np.array([ 
              [1, 1], 
              [2.5, 2],
              [3, 3.3],
              [4.2, 4.3],
              [5.5, 6]
])
print("Data: ", X)

scaler = StandardScaler()
Z = scaler.fit_transform(X)

pca = PCA(1)

pca.fit(X)

B = pca.transform(X)
print("\n Projected Data: \n", B)

Data:  [[1.  1. ]
 [2.5 2. ]
 [3.  3.3]
 [4.2 4.3]
 [5.5 6. ]]

 Projected Data: 
 [[-3.22076872]
 [-1.4811973 ]
 [-0.17282188]
 [ 1.36956317]
 [ 3.50522473]]

pca.explained_variance_ratio_

array([0.99403669])

plt.scatter(B, [0, 0, 0, 0, 0])

<matplotlib.collections.PathCollection at 0x7fa2c446ee50>

original

PCA가 가지는 의의 및 한계

PCA는 기본적으로 다음과 같은 가정을 가지고 데이터를 분석합니다. 첫번째로 큰 분산을 갖는 방향이 중요한 정보를 담고있다고 가정합니다. 위의 그림에서 보면 길쭉하게 늘어진 방향을 가장 중요한 방향으로 생각하고 그곳을 축(basis)으로 데이터들을 투영(projection)하게 됩니다. <br 두번째로는 우리가 찾은 주축(principal component)들은 서로 직교(orthogonal)한다고 가정합니다. PC1이 분산이 가장 큰 값을 갖는 축이라면, 그 다음 PC2는 무조건 이것과 직교하는 축을 찾는다는 것입니다.

PCA가 갖는 한계 역시 존재합니다. 먼저 정말로 큰 분산이 갖는 방향이 정말로 우리가 찾고자하는 중요한 방향인지 생각해보아야 합니다. PCA를 통해 추출해낸 주성분들은 낮은 분산을 보이면서 critical한 특성을 가지고 있을 daata들을 무시할 가능성이 있습니다. 각 데이터가 갖는 특성에 따라 우리는 주축을 달리 찾을 필요가 있습니다.
또한 PCA 주축간의 상관관계가 없다는 것이 data들 간의 독립성을 보장하진 않는다는 것입니다. 그리고 데이터의 분포가 정규성을 띄지 않는 경우 적용이 어렵고, 특히 분류 / 예측 문제에 대해서 데이터의 라벨을 고려하지 않기 때문에 효과적 분리가 어려운 단점을 가지고 있습니다.

Reference

https://bskyvision.com/236
https://nittaku.tistory.com/291
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=moojigai07&logNo=120186757908
https://angeloyeo.github.io/2019/07/15/Matrix_as_Linear_Transformation.html
https://analysisbugs.tistory.com/174?category=853972
https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-19-%ED%96%89%EB%A0%AC
https://firework-ham.tistory.com/44
https://m.blog.naver.com/qbxlvnf11/221323034856
https://angeloyeo.github.io/2019/07/27/PCA.html