Machine learning

AI, Machine Learning, and Deep Learning

AI

AI(Artificial intelligence, AI)는 인간의 학습능력, 추론능력, 지각능력을 컴퓨터에 인공적으로 구현하려는 컴퓨터과학의 세부분야입니다.

ML

기계 학습 또는 머신 러닝(Machine learning, ML)은 AI의 하위집합으로 컴퓨터가 경험을 통해 자동으로 개선하기 위해 학습할 수 있도록 하는 알고리즘과 기술을 개발하는 분야입니다.

DL

심층 학습 또는 딥 러닝(Deep learning, DL)은 여러 비선형 변환기법의 조합을 통해 높은 수준의 추상화(abstractions, 다량의 데이터나 복잡한 자료들 속에서 핵심적인 내용 또는 기능을 요약하는 작업)를 시도하는 기계 학습 알고리즘의 하위집합이며, 큰 틀에서 사람의 사고방식을 컴퓨터에게 가르치는 기계학습의 한 분야라고 이야기할 수 있습니다.

Machine learning의 종류

1. 지도학습(Supervised Learning)

label이 있는 데이터를 활용하여 input-output의 관계를 찾아 새로운 데이터에 대한 결과를 예측하는 학습방법입니다.

• 분류(Classification)

  outcome value가 discrete한 경우 사용하며, 주어진 input data의 category 또는 class를 예측하는 데에 활용됩니다.

• 회귀(Regression)

  outcome value가 real or continuous number인 경우 사용하며, 주어진 data들의 feature를 기준으로 연속된 값을 예측하는 문제에 활용됩니다.
  
  

지도학습 알고리즘

• KNN(K-Nearest Neighbor)
• Linear Regression
• Logistic Regression
• SVM
• Decision Tree
• Random Forest
• ANN (인공신경망) …..

2. 비지도학습(Unsupervised Learning)

지도학습과 달리, label이 없거나 제공되지 않은 data들을 비슷한 특징끼리 군집화하여 새로운 데이터에 대한 결과를 예측하는 학습방법입니다.

• 군집화(Clustering)

  주어진 데이터들의 특성들을 고려하여 유사도를 측정해 비슷한 특성을 가지는 데이터들을 그룹화하는 방법을 말합니다.

  • 주요 알고리즘

    1. k-means Clustering
    2. Mean Shift Clustering
    3. Expectation-Maximization(EM) Clustering using GMM(Gaussian Mixture Model)
    4. DBSCAN(Density Based Spatial Clustering Of Applications with Noise)
    5. Agglomerative Hierarchical Clustering …..

• 연관 규칙 학습(Association Rule Learning)

  data의 feature들 가운데 서로 연관성을 가지고 있는지 찾아내는 방법을 말합니다.

  • 주요 알고리즘

    1. Apriori
    2. Eclat…

• 차원축소

  특성이 많은 고차원의 data를 feature의 수를 줄이면서 꼭 필요한 특징을 포함한 데이터로 표현하는 방법을 말합니다. 또한 서로 상관관계가 있는 여러 특성을 합치는 것으로 볼 수 있어 특성추출이라고도 합니다.

  • 주요 알고리즘

    1. PCA(principal Component Analysis)
    2. Kernel PCA
    3. LLE(Locally-Linear Embedding)
    4. t-SNE(t-distributed StochasticNeighbor Embedding)…

3. 강화학습(Reinforcement / Semisupervised Learning)

행동심리학에서 나온 이론으로, 주어진 환경 속에서 정의된 Agent가 상황마다 선택이 가능한 경우의 수들 중 보상을 최대화하는 ‘경우의 수’ 또는 ‘경우의 수들의 선택순서’를 찾아가며, 최대의 보상을 받을 수 있는 경우의 수를 찾는 방법을 말한다.
즉, 주어진 Environment에서 Agent가 reward를 극대화하기 위해 최적의 Action을 찾아가는 학습과정이라고 할 수 있습니다.

• 주요 알고리즘

  1. Q-Learning
  2. DQN(Deep Q-Network)
  3. A3C
  4. PPO(Proximal Policy Optimization) ….

Clustering Analysis

Clustering 목적

서로 특성이 유사한 데이터들은 같은 그룹, 서로 특성이 다른 데이터들은 다른 그룹으로 나눠 그룹화를 하는 것입니다.

Clustering 알고리즘은 다음 두가지 조건을 충족하는 ‘기준’을 가지고 있어야 합니다.

1. 몇 개의 그룹으로 나누어 분류할 것인가
2. 데이터의 특성 유사도는 어떤 기준을 가지고 정의할 것인가

얼마나, 어떻게 유사한지에 따라 군집을 나누기 때문에, 데이터셋을 요약/정리하는데 있어서 큰 활용가치가 있습니다.
하지만 동시에 정답을 보장하지 않기에, 예측을 위한 모델링에 사용되기 보다는 EDA를 위한 방법으로 많이 활용됩니다.
객관적으로 올바른, 확실한 클러스터링 알고리즘은 없으며, 데이터에 따라 그에 맞는 알고리즘을 선택하는 것이 정답입니다.

K-means Clustering

K-means clustering 알고리즘은 다음과 같은 ‘기준’으로 구성되어 있습니다.

1. K개의 그룹으로 군집화진행 (주어질 파라미터) -> dataset에서 찾을 클러스터 수
2. “Means”를 기준으로 유사도를 측정 -> 각 data로부터 그 data가 속한 cluster의 중심까지의 평균거리를 유사도의 척도로 판단
   

즉, data를 data와 k개의 cluster의 중심까지의 거리가 가장 최소화하는 cluster로 그룹화해주는 알고리즘입니다.
작동원리는 다음과 같습니다.

1. k개의 임의의 중심점(centroid)을 배치합니다.
2. data들을 각 cluster의 centroid와의 거리를 계산하여, 가장 가까운 cluster에 할당합니다.(초기 군집)
3. 각 cluster에 속한 data까지의 거리제곱합이 최소로 만들어줄 수 있는 점으로 cluster의 centroid를 재조정합니다.
4. 2,3번의 과정을 더이상 centroid가 update되지 않을 때까지 반복수행합니다.

의의 및 한계

1. 새로운 자료에 대한 탐색을 통해 의미있는 data를 찾을 수 있는 방법입니다.
2. 관측치간의 거리를 데이터의 형태에 맞게 정의를 해준다면, 적용이 간단하다는 장점이 있습니다.
3. 하지만 동시에 각 변수에 대한 가중치를 결정하는 것이 어렵고, 관찰 data들 사이의 거리를 정의하는 것또한 어렵다는 단점이 있습니다.
4. 또한 초기에 주어지는 K값에 따라 clutering의 결과가 달라집니다. 따라서 적절한 k값 선정또한 과제입니다.
5. 유사도를 중심으로부터 가까운 거리로만 판단하기 때문에 사전에 주어진 목적이 없어 결과해석또한 어렵습니다.

활용예시

위의 한계점을 가지고 있음에도 k-means clustering은 성향이 불분명한 시장분석, 트렌드와 같이 명확하지 못한 분류기준을 가진 data분석, 패턴인식 및 음성인식 기본기술, 관련성을 알 수 없는 초기 데이터 분류 등에 활용이 되고 있습니다.

Python tutorial

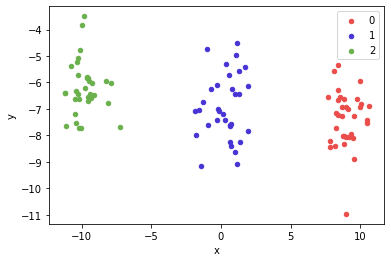
다음과 같이 임의의 점들이 있고, label이 있다고 생각해보겠습니다.

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

x, y = make_blobs(n_samples = 100, centers = 3, n_features = 2)
df = pd.DataFrame(dict(x = x[:, 0], y = x[:, 1], label = y))

colors = {0 : '#eb4d4b', 1 : '#4834d4', 2 : '#6ab04c'}
fig, ax = plt.subplots()
grouped = df.groupby('label')
for key, group in grouped:
    group.plot(ax = ax, kind = 'scatter', x = 'x', y = 'y', label = key, color = colors[key])
plt.show()     

# k-means clustering을 해주기 위해 reset
# 3개의 클러스터로 구분해보겠습니다.
points = df.drop('label', axis = 1) # label 삭제 
plt.scatter(points.x, points.y)
plt.show()

from sklearn.cluster import KMeans 
kmeans = KMeans(n_clusters = 3)
kmeans.fit(x)
labels = kmeans.labels_

new_series = pd.Series(labels)
points['clusters'] = new_series.values

def get_centroids(df, column_header):
  new_centroids = df.groupby(column_header).mean()
  return new_centroids

def plot_clusters(df, column_header, centroids):
  colors = {0 : 'red', 1 : 'cyan', 2 : 'yellow'}
  fig, ax = plt.subplots()
  ax.plot(centroids.iloc[0].x, centroids.iloc[0].y, "ok") # 기존 중심점
  ax.plot(centroids.iloc[1].x, centroids.iloc[1].y, "ok")
  ax.plot(centroids.iloc[2].x, centroids.iloc[2].y, "ok")
  grouped = df.groupby(column_header)
  for key, group in grouped:
      group.plot(ax = ax, kind = 'scatter', x = 'x', y = 'y', label = key, color = colors[key])
  plt.show()

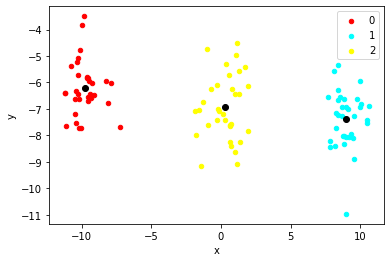
new_centroids = get_centroids(points, 'clusters')
plot_clusters(points, 'clusters', new_centroids)

# k를 모를 때 적절한 k값 찾기
sum_of_squared_distances = []
K = range(1, 15)
for k in K:
    km = KMeans(n_clusters = k)
    km = km.fit(points)
    sum_of_squared_distances.append(km.inertia_)
    
plt.plot(K, sum_of_squared_distances, 'bx-')
plt.xlabel('k')
plt.ylabel('Sum_of_squared_distances')
plt.title('Elbow Method For Optimal k')
plt.show()

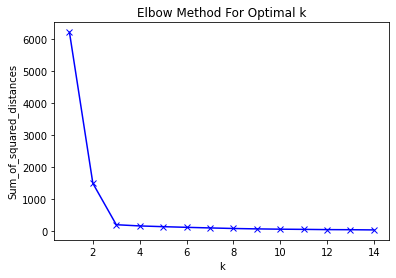
k값이 3이상부터 큰 차이가 없음을 확인할 수 있습니다.

DBSCAN clustering

k-means clustering의 경우 초기 중심값, k값에 크게 영향을 받고, noise와 outlier 에 몹시 민감하다는 단점을 가지고 있습니다. 이를 상대적으로 해결하고자 한 방법이 DBSCAN clustering입니다.

DBSCAN의 경우 eps-neighbors, MinPts를 사용하여 군집을 결정합니다.
eps-neighbors는 한 data를 중심으로 epsilon 거리 이내에 data들을 한 군집으로 인식하는데 이때 epsilon값을 의미합니다.
또한 구성된 군집은 MinPts값보다 많거나 같은 수의 data를 가져야합니다. 즉 각 군집에는 최소한의 data수가 있어야 합니다. 그렇지 않으면 군집전체를 noise, outlier로 취급합니다.

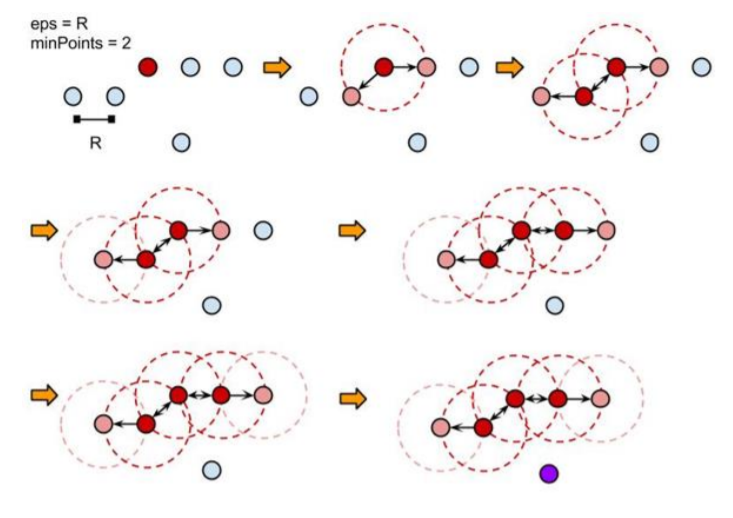
의의 및 한계

원형이 아닌 데이터들의 군집을 잘 분류해내고, 이상치에도 반응을 하지 않는 장점이 있습니다. 또한 cluster의 밀도에 따라서 연결하기 때문에, 기하학적인 분포를 가지는 data들의 군집화도 쉽게 할 수 있습니다.

하지만 역시 시작점과, epsilon값에 따라 성능이 좌우되는 한계를 가지고 있습니다. 또한 epsilon거리를 기준으로 포함여부를 결정하다보니 군집별로 구성하는 밀도가 다를 경우, clustering을 잘못할 가능성이 높아집니다.

활용예시

공학에서 noise 도는 이상치 검출할 때 활용됩니다.

Python tutorial

#시각화를 위해 세개의 feature만 사용하겟습니다.
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from mpl_toolkits.mplot3d import Axes3D
from sklearn.cluster import DBSCAN
import seaborn as sns

iris = datasets.load_iris()
labels = pd.DataFrame(iris.target)
labels.columns=['labels']
data = pd.DataFrame(iris.data)
data.columns=['Sepal length','Sepal width','Petal length','Petal width']
data = pd.concat([data,labels],axis=1)
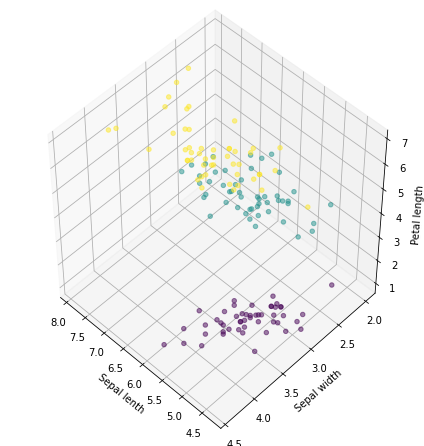
active_data = data[['Sepal length', 'Sepal width', 'Petal length', 'labels']]

fig = plt.figure( figsize=(6,6))
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
ax.scatter(active_data['Sepal length'],active_data['Sepal width'],active_data['Petal length'],c=active_data['labels'],alpha=0.5)
ax.set_xlabel('Sepal lenth')
ax.set_ylabel('Sepal width')
ax.set_zlabel('Petal length')
plt.show()

# create model and prediction
feature = active_data[['Sepal length','Sepal width', 'Petal length']]
model = DBSCAN(min_samples=6)
predict = pd.DataFrame(model.fit_predict(feature))
predict.columns=['predict']

# concatenate labels to df as a new column
result = pd.concat([feature,predict],axis=1)

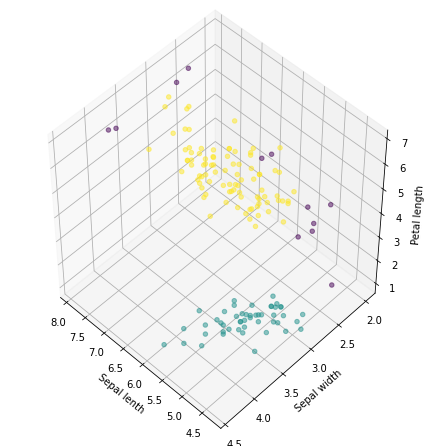
fig = plt.figure( figsize=(6,6))
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
ax.scatter(result['Sepal length'],result['Sepal width'],result['Petal length'],c = result['predict'],alpha=0.5)
ax.set_xlabel('Sepal lenth')
ax.set_ylabel('Sepal width')
ax.set_zlabel('Petal length')
plt.show()

ct = pd.crosstab(data['labels'],r['predict'])
print (ct)

predict  -1   0   1
labels             
0         1  49   0
1         6   0  44
2         5   0  45

Reference

https://michigusa-nlp.tistory.com/27
https://firework-ham.tistory.com/26
https://ebbnflow.tistory.com/165
https://gentlej90.tistory.com/20
https://hleecaster.com/ml-kmeans-clustering-concept/
https://muzukphysics.tistory.com/entry/ML-13-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-k-means-Clustering-%ED%8A%B9%EC%A7%95-%EC%9E%A5%EB%8B%A8%EC%A0%90-%EC%A0%81%EC%9A%A9-%EC%98%88%EC%8B%9C-%EB%B9%84%EC%A7%80%EB%8F%84%ED%95%99%EC%8A%B5
https://todayisbetterthanyesterday.tistory.com/59
https://bcho.tistory.com/1205