회귀와 분류
분류(Classification)
- outcome value가 discrete한 경우 사용하며, 주어진 input data의 category 또는 class를 예측하는 데에 활용됩니다.
회귀(Regression)
- outcome value가 real or continuous number인 경우 사용하며, 주어진 data들의 feature를 기준으로 연속된 값을 예측하는 문제에 활용됩니다.
기계학습 전초단계
데이터 분할
머신러닝 또는 딥러닝 모델을 학습시킬 때, 데이터 전부를 학습에 사용하지 않습니다. 모델학습에 이용할 train data set, 모델검증에 이용할 validation data set, 모델평가에 이용할 test data set으로 분할하여 사용합니다.
일반적으로 전통적인 머신러닝 학습에서는 아래와 같은 비율로 분할합니다.
\begin{align} train set : validation set : test set = 6 : 2 : 2 \end{align} \begin{align} train set : test set = 8 : 2 \end{align} \begin{align} train set : test set = 7 : 3 \end{align}
하지만 최근에는 빅데이터를 다루다보니, 데이터의 수가 충분하다면 데이터를 최대한 학습에 사용해도 무방하다는 이야기가 나옵니다. 예를 들어 백만개의 데이터가 있을 때, 1%만 해도 만개이다 보니, validation or test의 개수로 충분하다는 것입니다.
[출처: 앤드류 응 교수 딥러닝 강의]https://www.youtube.com/watch?v=_Fe5kKmFieg&list=PLkDaE6sCZn6E7jZ9sN_xHwSHOdjUxUW_b&index=7

데이터 분할 목적
ML 모델의 목표는 새로운 데이터를 잘 예측하기 위해 기존 데이터로 학습시켜 예측력을 높이는데 있습니다. 여러 알고리즘, 여러 모델중 최종 모델을 선정하기 위해서는 모델들의 성능평가가 필요합니다. 따라서 기존 데이터를 분할해, 학습된 모델들을 검증할 validation data set, 최종으로 선정된 모델의 성능평가할 test data set으로 활용합니다.
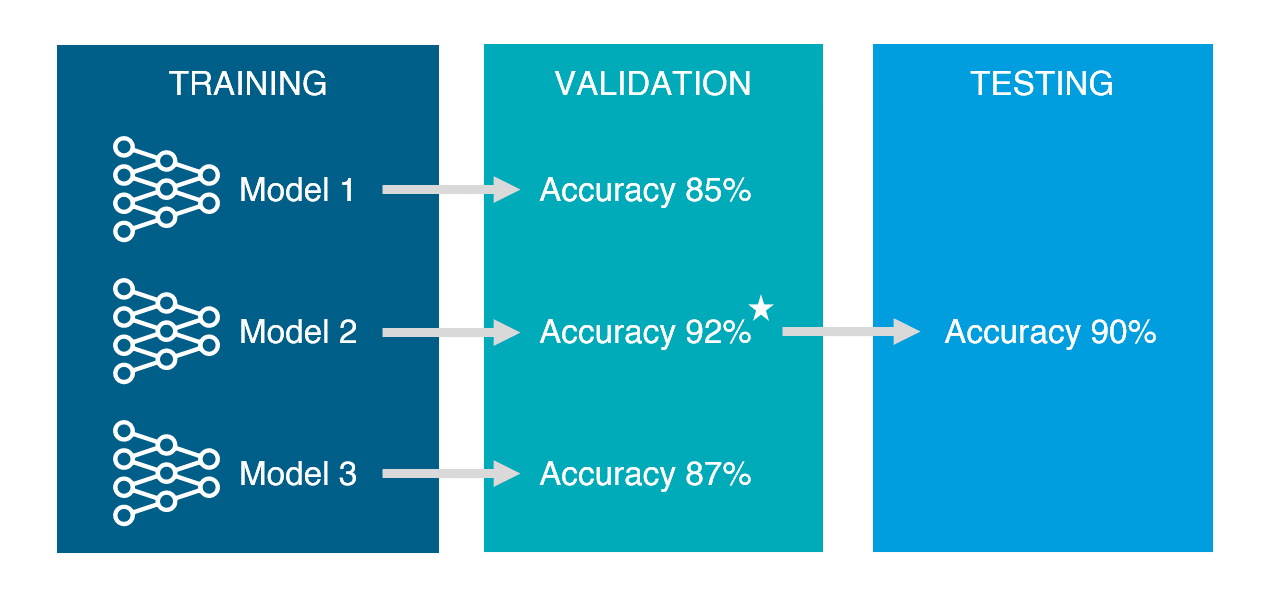
데이터 분할할 때 유의할 점
각 data set으로 분할할 때, 쏠림현상이 있지 않게 분할해야 한다. 예를 들어 train data는 그룹 A,B,C data가 있는데, test data에 그룹D가 있으면 안된다. -> shuffle을 통해 섞어준 후 랜덤하게 분할하는 방법이 도움이 될 수 있습니다.
참고사항
train data set class imbalance 문제: train data를 구성하는 class들의 비율이 적당히 맞아야 합니다. majority class에 과도하게 학습될 경우, minority class에 대해 예측할 확률이 현저히 낮아집니다. -> accuracy로만 평가할 문제가 아니라면, weight balancing, Over/Under sampling을 통해 클래스 불균형문제를 해결한 후 데이터 분할을 해주어야 합니다.
Overfitting/Underfitting
Overfitting
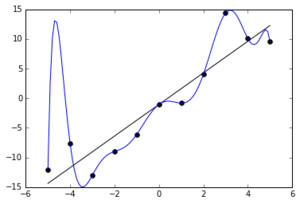
머신러닝 모델이 훈련데이터를 너무 잘 학습하여, 일반화가 되지 않는 문제를 overfitting이라고 합니다. 예를 들어 문제집, 기출문제로만 과도하게 학습되다보니, 문제집 정답은 잘 맞는데 새로운 문제를 풀 때, 생각보다 많이 틀리는 문제가 발생한 거라고 볼 수 있습니다.
실제로 훈련데이터에 noise나 oulier가 섞여있을 경우 이러한 데이터또한 학습을 하여 문제가 될 수 있습니다.
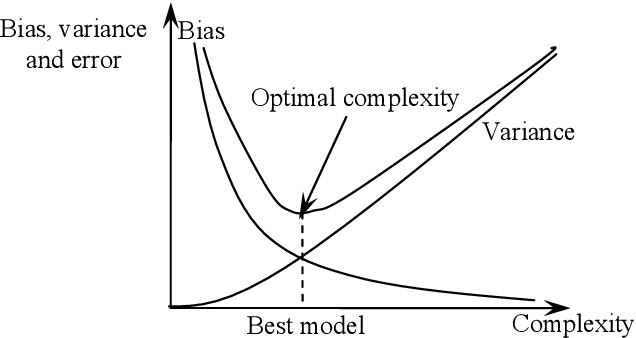
해결방안 : validation data set을 활용하여 학습된 모델을 검증하여, 일반화가 잘 이루어졌는지 평가하고, k-fold cross validation, regularization 등을 반복하여 과도한 학습을 막아 해결합니다. 특히 regularization은 variance값을 낮추는 방법으로 overfitting을 해결합니다. 딥러닝에서는 ealry stopping, dropout같은 기법을 활용합니다.
Underfitting
머신러닝 모델이 학습을 심도있게 하지 못하여 데이터의 패턴, 특징 등을 찾아내지 못해 모델이 단순해진 경우를 말합니다.
해결방안: 훈련데이터의 더 많은 특징을 찾아 학습시킵니다. 또한 모델의 제약을 줄이고(규제 하이퍼파라미터 값 줄이기) overfitting이 되기 전의 시점까지 충분히 학습시킵니다. 또한 variance값이 높은 모델(decision tree, k-nn, svm)을 선택하는 방법이 있습니다.
One-hot Encoding
텍스트 데이터의 경우, 컴퓨터가 이해할 수 있는 숫자로 변환해줄 필요가 있습니다. 여러 Encoder중 One-hot encoding은 직관적이며 손쉽게 활용할 수 있습니다. One-Hot encoding은 범주형 데이터의 class 유형을 새로운 feature로 독립시켜 1,0,0,… 등으로 표현한 Encoding입니다. 다음 시각화자료를 보시면 이해하기 쉬우실 것입니다.
Linear Regression model
회귀모델 중 가장 기본이 되는 모델이 선형회귀 모델입니다. 독립변수 x에 대응하는 종속변수 y와 가장 비슷한 값 y’ 를 출력하는 모델을 선형 회귀모델이라고 합니다. x와 y의 갯수에 따라 종류가 나눠집니다. MSE(mean of squared error)값을 가장 적은 방향으로 계산하여 구합니다.

선형회귀모델을 만들기 위해서는 데이터들에 대한 가정이 필요합니다.
- 선형성
- 독립 변수와 종속 변수는 선형입니다.
- 독립변수 간의 독립성
-
독립변수 간에는 상관관계가 없습니다.
-
독립 변수 간에 다중공선성이 존재하지 않으며, 독립변수 중 어느 것도 모형 내 다른 독립 변수와의 선형 조합으로 나타낼 수 없습니다.
- 정규분포를 따르는 오차항 : E(u) = 0, u ~ N(0,1)
-
표본 오차는 일종의 확률 변수로서 일정한 분포를 따른다고 가정하며, 정규 분포를 따른다는 가정에서 기댓값은 0이 됩니다.
-
β0를 이용하여 항상 E(u)=0로 정규화할 수 있습니다.
-
오차항과 독립변수 간의 독립성 : E(u x) = E(u) =0
-
독립변수와 오차항은 서로 독립입니다. 독립변수로 오차항에 대한 어떤 정보도 설명할 수 없다는 의미입니다. 따라서 E(y x) = β0 + β1x로 나타낼 수 있습니다.
- 오차항 간의 독립성
-
오차항 간의 자기상관성이 존재하지 않습니다.
-
오차의 분산이 일정합니다(등분산성) : Var(u x) = E(u*ut) =s2 -
ut : 표본오차의 역행렬
- s : 분산(시그마)
Logistic regression model
로지스틱 회귀(Logistic Regression)는 회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘입니다.
비교


위의 두번째 그림처럼 0 또는 1로 구분해주는 역할을 하며 분류문제에 많이 사용됩니다.
Reference
https://modern-manual.tistory.com/19
https://hyjykelly.tistory.com/44
https://3months.tistory.com/414
https://icefree.tistory.com/entry/기초-통계-회귀모델-Regression-Model
https://hleecaster.com/ml-logistic-regression-concept/