Decision Tree Model
Decision Tree란?
Decision tree는 data들을 여러가지 조건을 순차적으로 적용하여 분할하는 알고리즘으로, 분류와 회귀 둘 다 사용할 수 있어 CART(Classification And Regression Tree)라고도 불리는 머신러닝 알고리즘입니다. 특히, white box model중 하나로 직관적이고 결정 방식을 이해하기 쉽습니다.
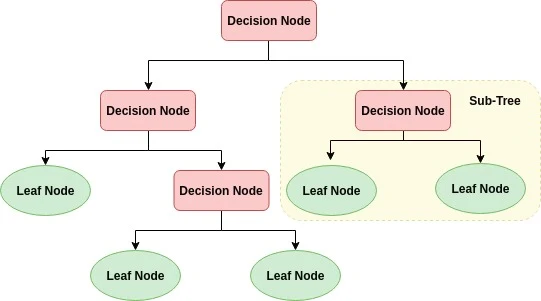
아래의 그림을 참고하면 Decision Node는 data를 분할할 조건이 표시된 node이고, Leaf Node의 경우 분할이 끝나 결정된 class값을 표현합니다. 더 분할할 필요가 있다면, Sub-tree를 다시 구성하여 class를 결정하도록 되어있습니다.
용어를 정리하자면 가장 상단 Decision Node를 Root node, class의 결정이 끝난 Leaf Node를 Terminal node, (자료구조중 tree구조이기에 두 용어가 혼용되기도 합니다.) Sub-Tree를 구성하는 Decision Node를 Intermediate node라고 합니다.
Decision node의 경우 여러 feature들의 결합을 통해 규칙을 만들어 sub-tree를 구성하게 되는데, 이러한 규칙이 복잡해지고 많아질수록 과적합이 일어날 가능성이 높아지기도 합니다. 이 부분이 Decision tree model의 단점이며, 이를 해결하고자 다음에 설명드릴 앙상블 모델(random forest model 등)이 나오기도 하였습니다.
Decision의 기준
Decision Tree model에서도 최선을 다하여 과적합을 막으려고 하는 노력이 있는데, 첫번째 방법으로 가능한 적은 decision node로 높은 예측 정확도를 가지는 것입니다. 한 번 분류할 때, 최대한 많은 data들이 분할이 될 수 있는 decision을 고르는 노력이라고 할 수 있습니다.
조금 더 어려운 용어를 사용하자면, Decision tree는 분류 후의 각 영역의 불순도(impurity) 또는 불확실성(uncertainity)이 최대한 감소하도록 하는 방향으로 학습합니다.
불순도를 측정하는 척도로써, 다음과 같은 지수를 사용합니다.
- Entropy : 열역학에서는 Entropy를 분자의 무질서함을 측정하는 척도로 사용하고 있습니다. 질서 정연하면 Entropy가 0에 가깝습니다. 이처럼 data집합의 혼잡도를 측정하는 척도로 서로 다른 값들이 섞여 있으면 entropy가 높고, 같은 값끼리 모여있으면 entropy가 낮다라고 판단할 수 있습니다. 사실 decision을 결정하는 척도로는 Information Gain을 사용합니다. Information Gain은 1에서 entropy를 뺀 값입니다.
- 수식: \begin{align} \mathrm {H}=-\sum_{i=1}^{n} {p_{i}\log_{2}(p_{i})} \end{align} \begin{align} Information \; Gain = 1 - {H} \end{align}
- Gini Index: 서로 다른 값들이 섞여 있는 영역에서 잘못 분류된 특정 기능의 확률을 계산합니다.
- 수식: \begin{align} \mathrm {G.I}= 1 - \sum_{i=1}^{n} {p_{i}^2} \end{align}
scikit-learn 라이브러리에서는 default 값으로 gini를 사용하고, entropy로도 변경이 가능합니다. 두 기준은 실제로는 큰 차이는 없지만, gini가 조금 더 계산이 빠르다고 알려져 있습니다. 하지만 gini는 가장 높은 빈도 클래스를 한쪽 branch로 고립시키는 경향이 있는 반면, entropy는 조금 더 균형 잡힌 tree를 만들어 냅니다
한편, decision tree의 회귀모델은 mse을 최소화하도록 분할합니다.
가지치기(Pruning)
Decision tree의 모든 terminal node의 순도가 1인 상태를 full tree라 하는데, 이는 훈련 데이터에 대해 학습을 하여 순도가 1을 형성했기 때문에, 새로운 데이터에 대해서는 과적합을 형성할 가능성이 몹시 높습니다. 따라서 적당한 수준에서 terminal node를 결합해줄 필요가 있습니다. 이를 사후 pruning이라 합니다.
그리고 Decision tree은 훈련되기 전에 파라미터 수가 결정되지 않기 때문에 비파라미터 모델이라고 부르곤 합니다. 모델의 구조가 데이터에 따라 유연하게 변경이 된다는 말입니다. 하지만 과대적합을 피하기 위해서는 결정트리의 자유도를 제한할 필요가 있습니다. full tree를 형성하기 전, 여러 규제를 통해 결정 트리의 자유도를 제한하여 tree의 분기를 막는 것을 사전 pruning이라 합니다.
규제방법으로 max_depth(tree의 최대 깊이 제어), min_samples_split(분할되기 위해 노드가 가져야 하는 최소 샘플 수), min_samples_leaf(leaf node가 가지고 있어야 할 최소 샘플 수), max_features(각 노드에서 분할에 사용할 특성의 최대 수) 등등이 있습니다.
장/단점
장점 : 선형회귀모델과 다르게 데이터 전처리(특성의 스케일을 맞추거나, normalization)이 거의 필요하지 않습니다. 또한 특성들간의 상관관계가 많아도 영향을 받지 않습니다. 결정방식을 이해하기 쉽습니다. 분류, 회귀 전부 사용가능하며, 수치형, 범주형 데이터 역시 모두 가능합니다.
단점 : 과적합에 의해 예측 성능이 저하된다. 모든 분할이 축에 수직이기 때문에 훈련 데이터의 회전에 민감합니다. 훈련 데이터에 있는 작은 변화에도 매우 민감합니다.
선형회귀 모델에서는 각 독립변수의 회귀계수(coefficients)가 가중치로서 특성의 중요도를 판가름할 수 있었습니다. 결정트리 모델에서도 특성중요도를 확인할 수 있습니다. scikit-learn에서는 Gini Importance를 이용하여, gini impurity를 얼마나 감소시키는 지에 따라 각 feature의 중요도를 측정합니다.
앙상블 학습(Ensemble Learning)
앙상블의 아이디어는 집단지성과 비슷합니다. 하나의 학습모델로 예측하는 것보다 여러 학습모델로부터 결과예측을 수행해 좋은 결과를 획득하는 것을 목표로 하고 있습니다.
이러한 여러 학습모델들을 묶어 Ensemble이라하여, 위와 같은 방법으로 학습하는 것을 Ensemble Learning, 학습하는 알고리즘을 Ensemble method라고 합니다.
이미지, 음성 등의 비정형 데이터의 분류는 딥러닝이 뛰어난 성능을 보이지만, 정형 데이터의 분류 경우 Ensemble 방법이 상당한 성능을 나타내고 있습니다. 대표적으로 random forest model, GBM 등이 있습니다.
앙상블의 종류
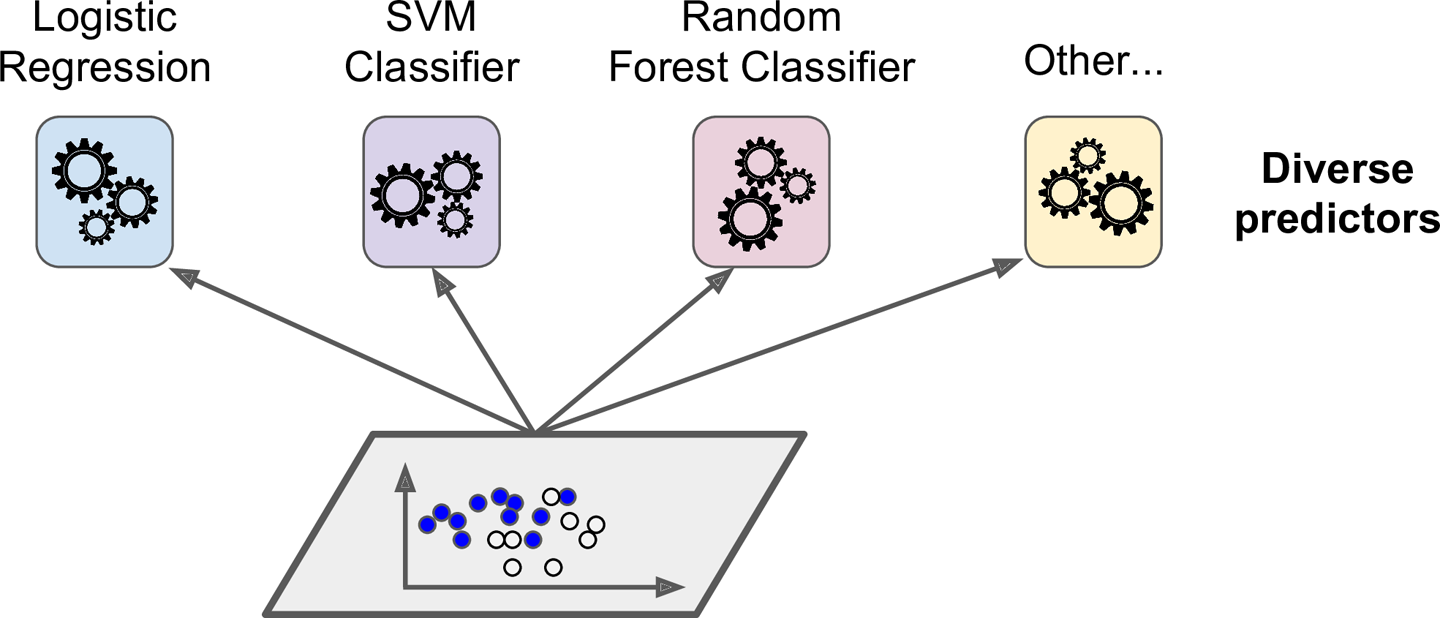
- Voting: 전체 훈련데이터셋에 대해 서로 다른 알고리즘의 classifier들을 통한 예측결과를 모아서 가장 많이 선택된 class를 최종 class로 결정하는 hard voting, 모든 classifier들이 class의 확률을 예측할 수 있다면(predict_proba() 사용가능하면) 각 예측 확률을 평균내어 확률이 가장 높은 class를 최종 class로 결정하는 soft voting이 있습니다.
Voting:
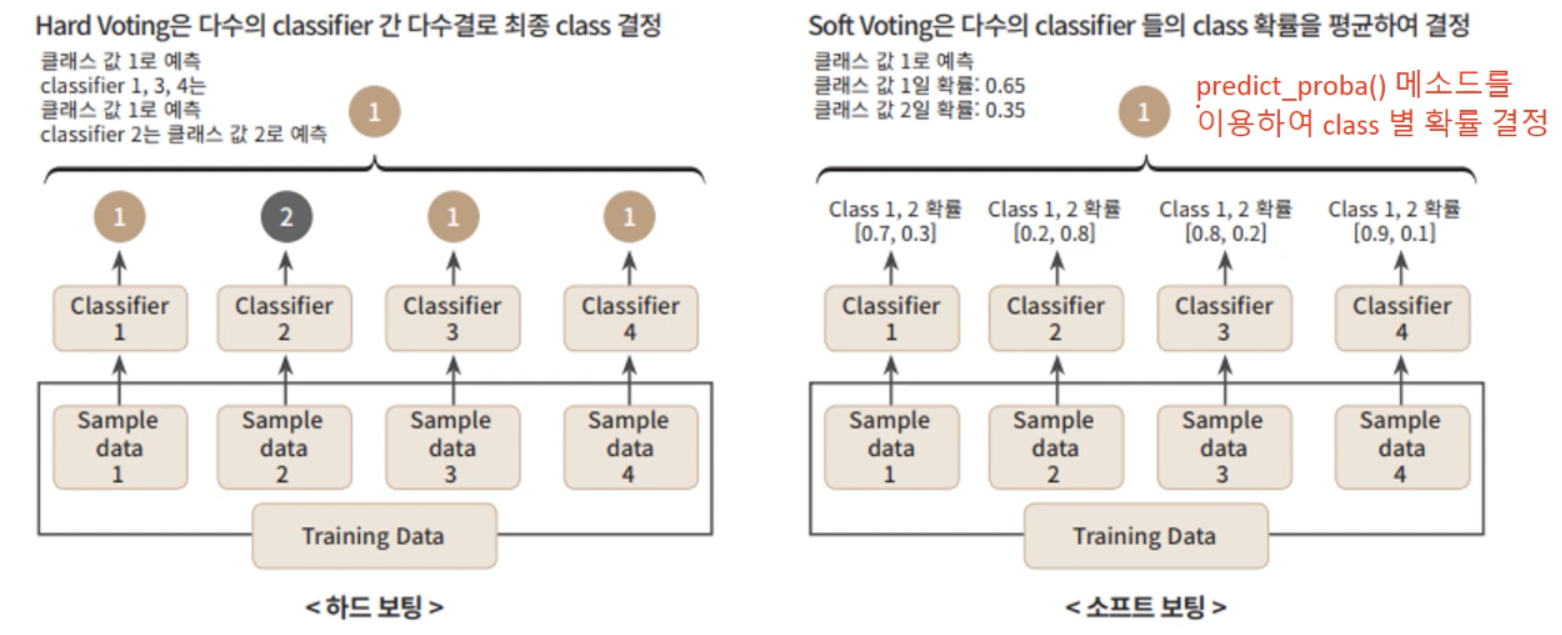
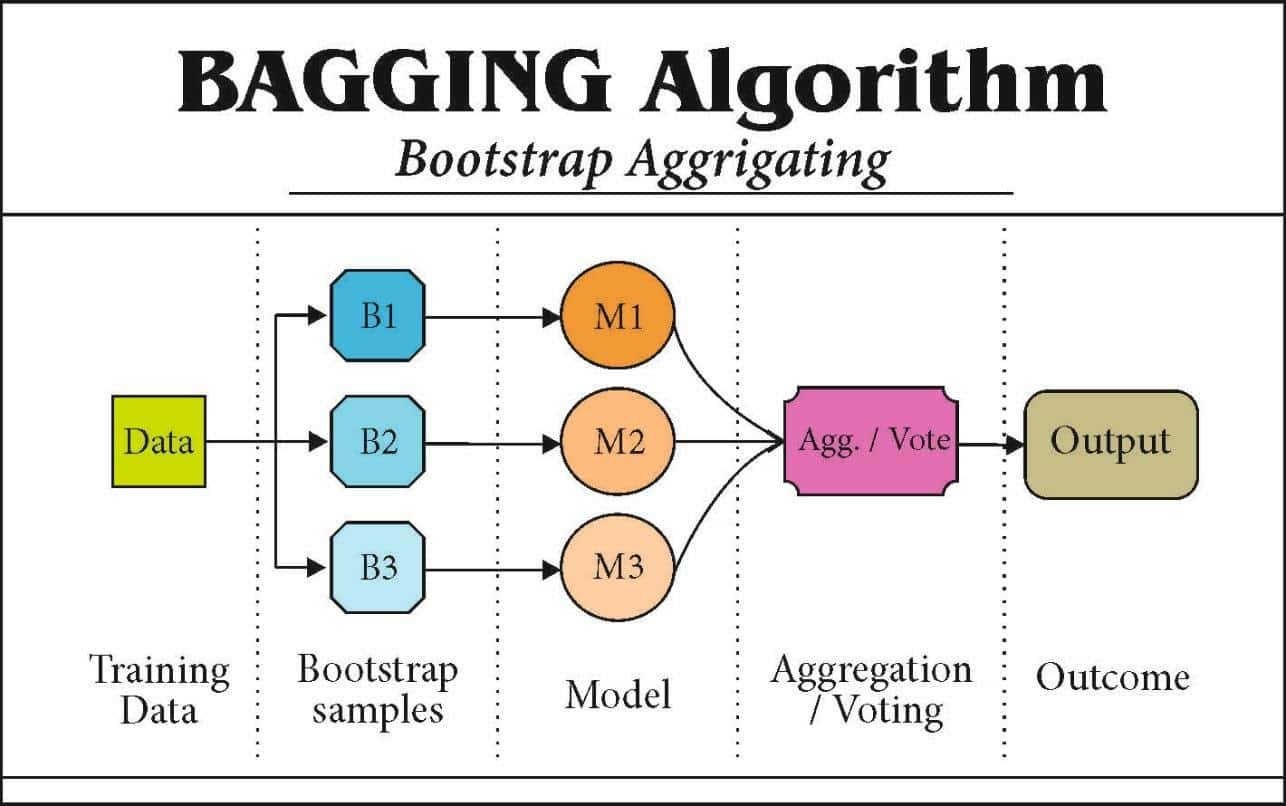
- Bagging: Boostrap aggregating의 줄임말로, 훈련 데이터셋을 전체가 아닌, 서브셋을 무작위로 다양하게 구성한 뒤, 같은 알고리즘의 classifier을 사용하여 각기 다르게 학습시켜 결과를 voting하는 방법입니다. 서브셋을 구성할 때, 중복을 허용하여 샘플링을 하는 방식을 boostrapping이라 하며, 구성된 sample은 boostrap sample이라합니다.
(중복을 허용하지 않고 샘플링하는 방식을 pasting이라 하는데, 따로 다루지 않겠습니다. bagging이 편향은 조금 더 높지만, 다양성을 추가하여, 분산값을 감소시켜 더 선호됩니다.)
Bagging:
- Boosting: 약한 학습모델을 여러 개 연결하여 강한 학습모델을 만드는 Ensemble 방법입니다. boosting의 아이디어는 이전 학습모델을 보완해나가면서 일련의 예측모델을 학습시키는 것입니다. 대표적으로 AdaBoost(adaptive boosting)와 Gradient boosting이 있습니다.
- AdaBoost: 이전 모델이 과소적합했던 훈련 샘플의 가중치를 더 높여 가중치를 update하는 방식으로 보완해나가는 Boosting방법입니다.
- Gradient boosting: 비용 함수를 최소화하기 위해 이전 예측모델이 만든 잔여오차에 새로운 예측모델을 학습시키며, 예측모델의 모델 파라미터를 조정해가는 방식으로 보완해나가는 Boosting방법입니다.
Random Forest Model
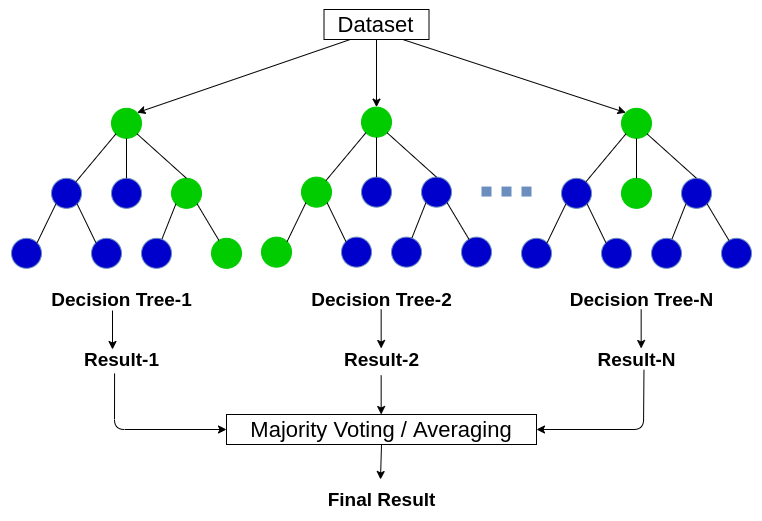
배깅 알고리즘으로 대표적인 앙상블 모델로 Random Forest Model이 있습니다. 이름에서 알 수 있듯이 기반 알고리즘은 Decision Tree model입니다. Decision Tree model이 분류와 회귀 둘 다 사용가능하므로, Random Forest model또한 분류, 회귀 둘 다 사용가능하며, 분류에서는 Voting방식을, 회귀에서는 averaging방식을 선택하고 있습니다.
또한, Decision Tree model에서는 전체 특성 중 최적의 특성을 고르고 특성 조건에 따라 분할을 하였지만, Random forest에서는 무작위로 sampling한 특성 후보 중에서 최적의 특징을 찾는 방식으로 무작위성을 더 주입하여 분할합니다.
장/단점
장점: 여러 모델을 CPU병렬적으로 처리하여 학습시킬 수 있어 빠른 학습이 가능합니다.
단점: 하이퍼 파라미터가 너무 많아, 튜닝을 위한 시간이 많이 소모됩니다. 텍스트 데이터같이 매우 차원이 높고 희소한 데이터에는 잘 작동하지 않습니다.
Reference
참고도서 : 핸즈온 머신러닝
https://nicola-ml.tistory.com/93
https://ratsgo.github.io/machine%20learning/2017/03/26/tree/
https://nicola-ml.tistory.com/95?category=861724
https://tensorflow.blog/%ED%8C%8C%EC%9D%B4%EC%8D%AC-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D/2-3-6-%EA%B2%B0%EC%A0%95-%ED%8A%B8%EB%A6%AC%EC%9D%98-%EC%95%99%EC%83%81%EB%B8%94/