모델 평가지표
우리는 하나의 데이터 셋에 대하여 다양한 모델을 학습시켜 결과를 예측할 것입니다. 이 때, 어떤 모델이 더 나은 모델인지 판단하기 위해서는 모델성능을 평가하는 평가지표가 필요합니다. 머신러닝에서는 다음과 같은 성능 평가 지표(Evaluation Metrics)를 활용하여 모델을 평가합니다.
- Regression(회귀)
- MSPE
- MSAE
- R Square
- Adjusted R Square
- …
- Classification(분류)
- Accuracy(정확도)
- Precision(정밀도)
- Recall(재현율)
- F1 score
- ROC, AUC
각 학습법에 따라 평가지표가 다르고, 각 데이터마다 중요하게 여기는 point가 다를 것입니다. 따라서 데이터의 형태에 따라 맞는 평가지표를 선택하여야 합니다.
이 중에서 분류에 해당되는 평가지표를 살펴보겠습니다.
Confusion Matrix(오차행렬)
분류에 대한 문제를 해결할 때, 평가지표를 살펴보기 전에 Confusion Matrix를 알아보겠습니다.

가장 쉬운 이진 분류를 나타내면, 위의 그림과 같은 4가지의 경우가 발생합니다.
- TP(True Positive) : 실제 True를 예측결과 Positive로 정답을 예측한 경우
- FN(False Negative) : 실제 False를 예측결과 Negative로 정답을 예측한 경우
- TN(True Negative) : 실제 True를 예측결과 Negative로 오답을 예측한 경우
- FP(False Positive) : 실제 False를 예측결과 Positive로 오답을 예측한 경우
이 4가지의 경우로 각 평가지표를 나타내보겠습니다.
Accuracy(정확도)
\begin{align} Accuracy = \frac{ TP + FN}{TP+FN+TN+FP} \end{align}
Accuracy란 전체 데이터에 대해서 정답을 예측한 확률입니다. TP와 FN의 경우 정답을 맞춘 경우에 해당이 됩니다. 일반적이고 가장 간단하게 살펴볼 수 있는 평가지표입니다. 하지만 Accuracy의 경우 Imbalanced한 데이터를 다루게 될 때, 큰 단점이 나타납니다. Majority class에 대해서 학습된 ML 모델이 예측을 무조건 Majority class로 예측을 하다보면 Accuracy는 높게 나오지만, Minority class에 대한 예측은 꽝일 수 있습니다.
이처럼 bias가 존재하는 데이터에 대해 Accuracy는 신뢰할 수 없는 지표가 되고, 이를 Accuracy Paradox라고 부릅니다.
이를 해결하기 위해 Precision(정밀도), Recall(재현율)을 살펴봅니다.
Precision(정밀도)
\begin{align} Precision = \frac{TP} {TP+FP} \end{align}
Precision은 예측결과가 Positive인 경우, 실제로도 True일 확률입니다. 1에 가까울 수록 실제 True를 Positive로 잘 예측했다는 지표입니다.
Recall(재현율)
Recall은 sensitivity(민감도)라고도 부릅니다.
\begin{align} Recall = \frac{TP} { TP + FN} \end{align}
실제 정답을 맞춘 경우 중 positive로 맞춘 경우일 확률입니다.
Precision과 Recall의 경우 둘 다 분자로 TP를 받고 있는 점에서 Positive로 예측했을 때, 실제 True인 경우를 중점을 두고 살펴보고 있습니다. 하지만 Precision의 경우, Model의 입장에서 Positive로 예측한 경우를 분모로 받고, Recall의 경우, Data의 입장에서 True인 경우를 분모로 받고 있다는 점이 차이점입니다.
Model 평가입장에서는 두 지표가 모두 높으면 좋지만, 서로 trade-off관계를 가지고 있습니다. 분류를 할 때, Decision Fuction의 threshold value에 따라 True, False를 예측하는데, 낮은 Threshold value를 적용할 경우 Model이 True라고 예측할 가능성이 높아지고 TP, FP의 경우가 증가하여, 상대적으로 FN 이 감소하면서 Recall값이 증가합니다. 반대로 높은 Threshold value를 적용할 경우 Model이 False라고 예측할 가능성이 높아지면서 TN, FN이 증가하고, 확실한 경우에만 True라고 하니 상대적으로 FP는 감소하면서 Precision값이 증가합니다.
두 지표가 Trade_off관계를 가지고 있다보니 저희는 데이터와 주어진 문제상황에 따라 두 지표중 더 중요시하는 지표를 통해 Model의 성능을 평가하게 됩니다.
아래 그래프처럼 Recall-Precision 그래프를 그렸을 때, 보통 급격한 하강점이 나타날 때, 그 직전을 정밀도-재현율 값으로 선택합니다.

또는 두 지표의 조화평균 값을 통해 두 지표의 적당한 장점을 취하려고 평가지표도 있습니다. 바로 F1 score입니다.
F1 score
F1 score은 Precision과 Recall( = sensitivity)의 조화평균 값입니다.
\begin{align} F1 score = 2 * \frac {Precision * Recall} {Precision + Recall} \end{align}
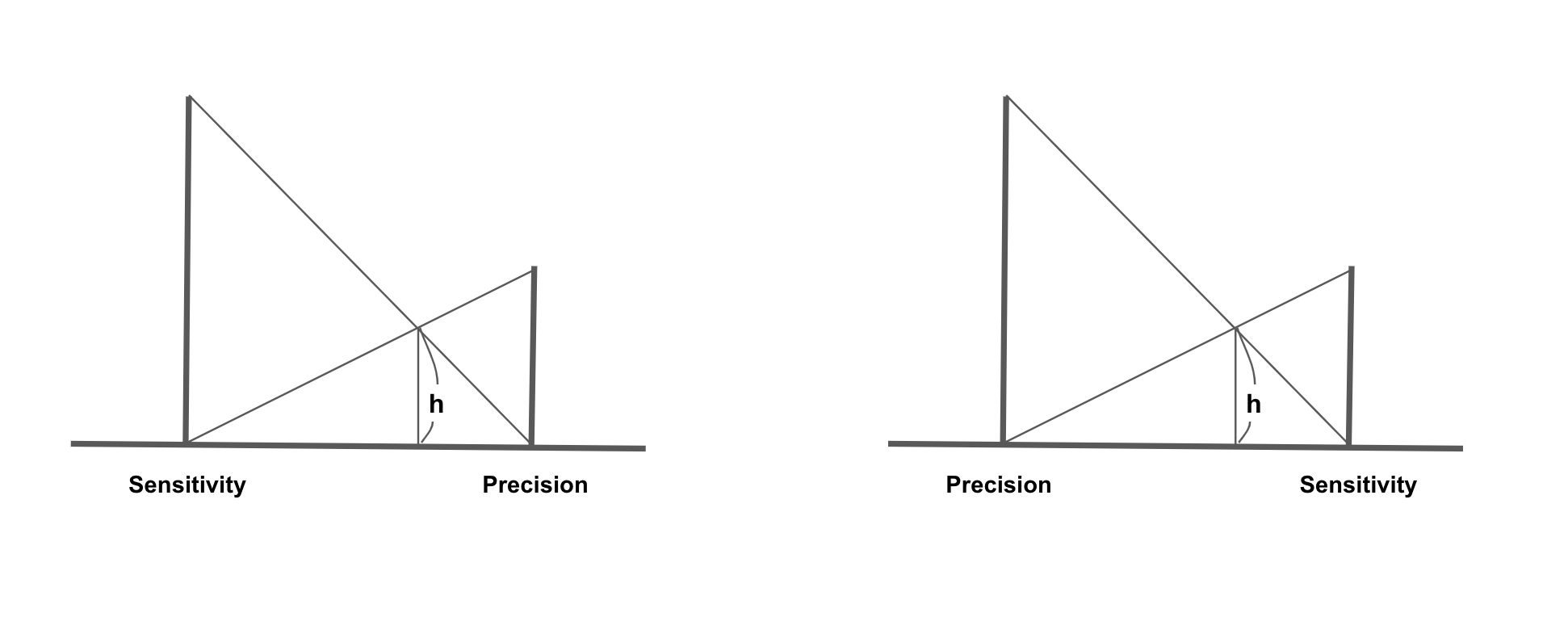
위의 사진과 같이 한쪽만 높아도 다른 한쪽의 크기에 따라 영향을 받으므로, 둘 다 높을 때 최대 값을 가지게 됩니다.
ROC (Receiver Operating Characteristic) curve & AUC (Area Under Curve)
ROC곡선은 FPR에 대한 TPR의 곡선으로 binary classfication에서 자주 사용하는 도구입니다.
FPR이란, Positive로 잘못 예측한 비율을 말합니다.
\begin{align}
FPR = \frac {FP} {FP + TN}
\end{align}
Confusion Matrix에서 구할 수 있는 Specificity(특이도)에 대해 살펴보면 실제 Negative를 얼마나 잘 예측했는가를 볼 수 있는 지표입니다.
\begin{align}
Specificity = \frac {TN} {FP + TN}
\end{align}
즉 FPR = 1- Specificity임을 알 수 있습니다.
그리고 TPR은 Recall의 다른 이름입니다. 정리하자면 ROC curve는 Threshold값에 따라 confusion Matrix가 결정될 때, Recall에 대한
1-Specificity 그래프라고 볼 수 있습니다.

ROC curve는 각 Threshold value에 대한 곡선 그래프다보니, 평가지표로서 수치를 표현하기 어렵습니다. 따라서 ROC curve에 대한 AUC를 구해 곡선 아래의 면적을 성능평가지표로 활용합니다.
random한 예측결과에 대해서는 ROC curve는 AUC가 0.5값을 가지는 직선입니다. 따라서 1에 가까울수록 성능이 좋다고 평가할 것이고, 0.5에 가까돌수록 예측모델이 꽝이라고 할 수 있습니다.
그렇다면 Precison-Recall curve와 ROC curve중 어느 것을 활용할지도 논의 대상이 될겁니다. 참고한 도서 ‘핸즈온 머신러닝’에서는 양성 클래스가 드물거나, 거짓음성보다 거짓양성이 중요할 때 Precision-Recall curve를 사용하고, 그렇지 않으면 ROC curve를 사용하는 것이 좋다고 말합니다.
ROC curve의 특징 중 하나가 class의 분포에 민감하지 않다는 것입니다. ROC curve의 변수 FPR, TPR이 class 분산에 영향을 받는 Accusracy 또는 Precision와는 다르게 독립적인 수치이기 때문입니다.
Reference
참고도서 : 핸즈온 머신러닝
참고blog :
https://ichi.pro/ko/jeongmildo-jaehyeon-yul-gogseon-seolmyeong-275702097098030
슘니의 무작정 따라하기 https://sumniya.tistory.com/26
우주 먼지의 하루 https://rk1993.tistory.com/entry/%EB%AA%A8%EB%8D%B8-%EC%84%B1%EB%8A%A5-%ED%8F%89%EA%B0%80-%EC%A7%80%ED%91%9C-%ED%9A%8C%EA%B7%80-%EB%AA%A8%EB%8D%B8-%EB%B6%84%EB%A5%98-%EB%AA%A8%EB%8D%B8
둔 앵거스 https://nicola-ml.tistory.com/88