ANOVA
지난 시간에 T-test를 통해 가설검정하는 이유와 예제를 살펴본 바 있습니다.
T-test는 1개 그룹의 평균이 특정 값과 같은지 (One-sample), 2개 그룹의 평균이 유의미하게 다른지(two-sample)를 살펴보는데 유용하게 활용되었습니다.
하지만 3그룹, 그 이상을 비교하고 싶다면 어떻게 해야 할까요? 단순하게 생각하면 그룹들을 각각 2개씩 짝지어 T-test를 하는 방법이 있을 것입니다. 이 방법의 경우type1-error가 발생합니다.
type1-error의 확률: \begin{align} {\alpha} = 1-(1-{\alpha}^c) \;\; ,({\alpha}는 \;0.05,\;\;c는\;총\;test횟수) \end{align}
test의 횟수가 늘어나면서 유의미한 결과를 얻지 못할 확률이 감소하여 귀무가설을 잘못 기각할 가능성이 0.05가 아닌 그 이상이 될 수 있습니다. 이러한 경우, ANOVA를 통해 검정을 합니다.
ANOVA란 무엇인가?
ANOVA는 ANalysis Of VAriance의 약어로 해석해보면 ‘분산분석’ 를 의미합니다. 3개 이상 그룹의 평균이 같은지, 다른지를 살펴보는데 왜 분산분석일까요?
말을 바꾸어보면 목표는 “3개 이상 그룹의 평균이 유의미하게 다른지 검정”하는 것이고, 방법으로 “분산을 분석하여 결론을 내린다” 라고 한다면 조금 더 와닿을 것입니다.
차근차근 ANOVA의 검정방법을 살펴보면서 이해해보도록 하겠습니다.
먼저 기본적으로 One-way ANOVA를 사용하기 위한 조건을 살펴보겠습니다.
- 종속변수는 연속형 변수, 독립변수는 이산형/범주형(Discrete/Categorical) 변수만 가능
- t-test와 마찬가지로 관측치가 정규분포를 따라야 한다.
- 구형성(등분산 가정)을 만족하여야 한다.
- 등분산가정은 일반적으로 관측치가 똑같은 경우에는 크게 문제가 되지 않는다.
- 샘플 수가 다른 경우, 각 그룹의 분산들 중, 최대값이 최소값의 1.5배 이상 크지 않다면 문제가 되지 않는다.
- 표본이 독립적이어야 한다
ANOVA와 F-value
위의 조건들을 만족하였다면, 본격적으로 F-value를 계산하여, F-분포를 확인 후 가설검정을 해보도록 하겠습니다.
-
One-way ANOVA (3개의 group, 10개(3개, 4개, 3개)의 관측치)
- H0 : 모든 그룹의 평균이 동일하다.
- H1 : 적어도 한 그룹의 평균은 다르다.
이 떄 F-value는 검정통계량 중 하나로, 두 가지의 분산(between variance, withiin variance)의 비율값을 뜻합니다. (이 이유로 분산분석이라 합니다.)
F-value = between variance / within variance
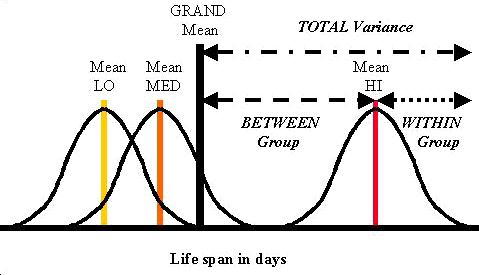
먼저 분산을 계산하기 위해서는 각 그룹의 평균(=group mean)과 전체 평균(=gross mean)이 필요합니다.
between variance는 전체 평균으로부터 각 그룹의 평균이 떨어진 정도를 나타내는 분산입니다. 이 값이 크다면 적어도 어떤 한 그룹은 다른 그룹과 평균이 다르다는 의미입니다.
betwwen variance = ( 3*(group1 mean - gross mean)^2
+ 4 * (group2 mean - gross mean)^2
+ 3 * (group3 mean -gross mean)^2
) / df1 # 자유도 df1 = (number of group -1)
하지만 betwwen variance가 얼마나 커야 통계적으로 의미가 있는 걸까요? 즉, 이 between variance가 우연히 클 가능성은 확률적으로 얼마가 되는지 확인하여야 합니다. 그래서 비교할 대상, within variance가 필요로 하게 됩니다.
within variance는 그룹내에서 각 관측치가 갖는 퍼짐 정도를 전부 구한 값이라고 할 수 있겠습니다.
수식을 보며 설명하겠습니다.
within variance = [ (group1_ob1 - group1 mean)^2
+(group1_ob2 - group1 mean)^2
+(group1_ob3 - group1 mean)^2
+(group2_ob1 - group2 mean)^2
+(group2_ob2 - group2 mean)^2
+(group2_ob3 - group2 mean)^2
+(group2_ob4 - group2 mean)^2
+(group3_ob1 - group3 mean)^2
+(group3_ob2 - group3 mean)^2
+(group3_ob3 - group3 mean)^2
] / df2 # 자유도 df2 = (총 관측치 개수 - 그룹 개수)
within variance가 가지는 의미를 다시 한번 살펴보면 t-test의 t-value 계산시의 분모의 표준편차와 같은 의미를 가지며, 즉 random한(무의미한) 변화의 정도라고 할 수 있습니다.
고로 between variance는 within variance보다 충분히 커야 우리는 between variance가 통계적으로 크다고 말할 수 있고, 적어도 어느 한 그룹의 평균 값이 다르다고 할 수 있습니다.
따라서 ANOVA에서는 F-value를 구하여 가설검정을 하게 됩니다.
F-분포
지금까지 F-value가 무엇이며, ANOVA에서는 F-value를 활용하여 가설검정을 한다는 것을 알아보았습니다. 하지만 위의 예시처럼 그룹내 모든 관측치를 사용하는 것이 아닌, 같은 그룹에서 같은 크기의 무작위 관측치를 여러 개 추출하여 동일한 One-way ANOVA를 실시하면 그 결과로 도출된 여러 F-값의 분포를 그릴 수 있습니다.

F-분포의 가정은 귀무가설이 참이라는 것이므로, 우리가 활용하는 F-value가 F-분포를 통해 충분히 높은 F-value인지 확률을 계산할 수 있습니다. 따라서 t-test때 처럼 p-value를 계산할 수 있고, 이 확률을 통해 귀무가설이 참이라는 가정을 채택하거나 기각하게 됩니다.
즉 충분히 큰 F-value를 가지고, ${\alpha}$가 0.05일때, 그 값이 F-분포중에서 , F-value가 발생할 확률이 희귀하여 그 이하라면 H0를 기각하고 H1를 채택하게 됩니다.
ANOVA -> POST-HOC
ANOVA는 결국 각 그룹의 평균들이 동일한지, 적어도 한 그룹의 평균은 다른지를 확인해줍니다. 하지만 이 결과가 어떤 그룹의 평균이 어떻게 다르다는 것인지 보여주지 않습니다. 뭐가 어떻게 다른지 확인하기 위해서는 ‘사후검정’이 필요합니다.
사후검정(POST-HOC)은 일종의 여러 다발의 t-test이며, type1-error를 발생시키지 않습니다. 각 그룹의 평균이 다른 그룹의 평균과 다를때 각각 비교가 가능합니다.
사후검정의 종류로는 Fisher’s LSD, Bonferroni, Sheffe, Turkey, Duncan이 있으며, 대부분의 경우 어떤 방법을 사용하여도 큰 차이가 없습니다.
import numpy as np
from scipy.stats import f_oneway
g1 = np.array([0, 31, 6, 26, 40])
print(np.mean(g1))
g2 = np.array([24, 15, 12, 22, 5])
print(np.mean(g2))
g3 = np.array([32, 52, 30, 18, 36])
print(np.mean(g3))
total = np.array([])
total = np.append(total,g1)
total = np.append(total,g2)
total = np.append(total,g3)
print(np.mean(total))
f_oneway(g1, g2, g3) # pvalue = 0.11
20.6
15.6
33.6
23.266666666666666
F_onewayResult(statistic=2.6009238802972483, pvalue=0.11524892355706169)
Chi squared test
${\chi}^2$ -검증은 수집된 자료가 모수적 통계분석을 사용하지 못할 경우 사용하는 비모수적 통계분석방법 중 하나로, 범주형 변수가 한개인 경우 변수내 group간의 동질성 여부를 통계적으로 검증하거나, 범주형 변수가 2개인 경우 변수 사이의 연관성을 통계적으로 검증하고자 할 때 사용됩니다.
특히 극단적인 outlier가 있는 경우 매우 유효한 방법입니다.
${\chi^2}$ 검증은 ${\chi^2}$ 분포라는 확률분포에 근거해서 표본 통계치의 유의성을 확률적으로 검증하는 방법으로, ${\chi}^2$ 분포의 가정을 따릅니다. 따라서 ${\chi}^2$ 분포를 생성하기 위해 사용한 자료와 조건이 같아야 합니다.
- 조건1: 종속변수가 명목척도, 즉 범주형 데이터여야 하고, data의 값은 개수이어야 합니다.
- 조건2: 기대빈도기 5이상 이어야 합니다. (범주를 합치거나, FIsher’ exact test or likelihood ratio test(G-test)를 하여야 합니다.)
- 조건3: 각 범주가 독립되어 서로 배타적이어야 합니다. 즉, 한 대상이 하나 이상의 범주에 들어갈 수 없음을 의미합니다.
Chi squared test
Chi squared test의 검정 통계량 ${\chi}^2$은 다음 수식으로 계산이 됩니다.
\begin{align} O : 관찰빈도(Observed frequency) \;\; E : 기대빈도(Expected frequency) \end{align}
\begin{align} {\chi}^2 = \sum \frac{(O-E)^2} {E} \end{align}
\begin{align} E = \frac{\text{전체 데이터 수}}{\text{# 데이터의 종류}} \end{align}
One-way ${\chi}^2$- test
H0: 각 범주가 나타날 빈도(확률)가 동일할 것이다.
H1: 범주들이 나타나는 빈도(확률)가 다를 것이다.
결론적으로 유의미하다는 의미는 사전에 정해진 기대빈도와 다르다는 의미입니다. 그래서 ${\chi}^2$-test를 적합도검증(goodness of fit)이라고 부르기도 합니다.
import numpy as np
from scipy.stats import chisquare
s_obs = np.array([[18, 22, 20, 15, 23, 22]]) # Similar
print('--- Similar ---')
chisquare(s_obs, axis=None) # One sample chi-square
--- Similar ---
Power_divergenceResult(statistic=2.3000000000000003, pvalue=0.8062668698851285)
ns_obs = np.array([[5, 23, 26, 19, 24, 23]])
print('--- not Similar ---')
chisquare(ns_obs, axis=None)
--- not Similar ---
Power_divergenceResult(statistic=14.8, pvalue=0.011251979028327346)
Two-way ${\chi}^2$- test
H0: 두 범주형 변수간 연관성이 없다( 상호독립이다)
H1: 두 범주형 변수간 연관성이 있다.
가장 단순한 형태는 2x2, contingency table을 활용하여 계산합니다. 다음 예시를 살펴보겠습니다.
| 예시 | 남자 | 여자 | 합계 |
|---|---|---|---|
| 고등학생 | 35 | 45 | 80 |
| 중학생 | 40 | 60 | 100 |
| 합계 | 75 | 105 | 180 |
[Step1] 두 범주가 독립적이라는 가정으로, 예측값구해보기
| 예시 | 남자 | 여자 |
|---|---|---|
| 고등학생 | 180 * (75 / 180) * (80 /180) | 180 * (105 / 180) * (80 /180) |
| 중학생 | 180 * (75 / 180) * (100 /180) | 180 * (105 / 180) * (100 /180) |
| 예시 | 남자 | 여자 |
|---|---|---|
| 고등학생 | 33.33 | 46.67 |
| 중학생 | 41.67 | 58.33 |
[Step2] ${\chi}^2$ value 구하기
| 예시 | 관측값 | 예측값 | $(O - E)^2 $ | $ \frac{(O - E)^2} {E}$ |
|---|---|---|---|---|
| 고등학생 & 남자 | 35 | 33.33 | 2.79 | 0.084 |
| 고등학생 & 여자 | 45 | 46.67 | 2.79 | 0.06 |
| 중학생 & 남자 | 40 | 41.67 | 2.79 | 0.067 |
| 중학생 & 여자 | 60 | 58.33 | 2.79 | 0.048 |
| ${\chi}^2$ 총 합 | 0.259 |
chi2_contingency 결과 해석
1 : $\chi^2$ statistic
2 : p-value
3 : degree of freedom
4 : expected value for Observed
from scipy.stats import chi2_contingency
obs = np.array([[ 35 ,45], [40, 60]])
print('---')
print(chi2_contingency(obs, correction = False)) # 위에서 계산한 것과 동일
---
(0.25714285714285634, 0.6120898800892574, 1, array([[33.33333333, 46.66666667],
[41.66666667, 58.33333333]]))
χ2 statistic이 수식으로 계산한 값과 거의 동일하고, p-value를 0.612로 구할 수 있었습니다. 따라서 귀무가설을 기각하지 못하므로, 두 범주형 변수는 연관성이 없다는 결론을 내릴 수 있습니다.
또한 χ2 검정 역시, 연관성의 유무만 판단할 뿐, 정도의 차이를 나타내진 않습니다. 두 변수가 연관성이 있을 경우, 상관관계를 알아볼 때 상관계수를 구하여 판단합니다.
베이즈의 정리
베이즈 정리의 의의
베이즈 정리는 새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신해나가는 방법이라고 할 수 있고, 근본적으로는 사전확률과 사후확률 사이의 관계를 나타내는 정리입니다.
전통적인 확룰관은 빈도주의(frequentism)이라고 볼 수 있는데, 베이지안주의 관점은 확률을 ‘주장에 대한 신뢰도’로 나타냅니다.
베이즈 정리는 기존의 통계학은 빈도주의 관점을 기반으로 모두 연역적인 사고를 기반으로 합니다. 즉, 집단에 대해 파악하고, 그 뒤의 계산을 통해 파생되는 결과물들을 수용하는 패러다임이었습니다.
반면, 베이지안 관점의 통계학은 사전확률과 같은 경험에 기반한 불확실성을 가지는 수치를 기반으로 하며, 이후 관찰하여 얻어지는 추가정보를 바탕으로 사전확률을 갱신합니다.
이와 같은 방법은 귀납적 추론방법이며, 베이지안주의는 추가적인 근거의 확보를 통해 진리로 더 다가갈 수 있다는 철학을 내포하고 있다는 점에서 기존 패러다임에 큰 변화를 일으켰다고 할 수 있습니다.
베이지안 이론 (Bayes Theorem)
아래는 베이지안의 핵심공식과 유도과정입니다:
\begin{align}
P(A|B) = \frac{P(A|B)}{P(B)}
\quad
P(B|A) = \frac{P(B|A)}{P(A)}
\end{align}
Since
\begin{align}
P(A \cap B) = P(B \cap A)
\end{align}
Therefore
\begin{align}
P(A|B) \cdot P(B) = P(B|A) \cdot P(A)
\end{align}
\begin{align}
P(A|B) = \frac{P(B|A)P(A)}{P(B)}
\end{align}
이는 $B$가 주어진 상황에서 $A$의 확률은 $A$가 주어진 상황에서의 $B$의 확률 곱하기 $A$의 확률, 나누기 $B$ 의 확률로 표현 됩니다.
$P(A)$ -> 사전 확률. B라는 정보가 업데이트 되기 전의 사전확률
${P(B|A)}$ -> likelihood
${P(A|B)}$ -> 사후 확률. (B라는 정보가 업데이트 된 이후의 사(이벤트)후 확률)
베이지안 예제
평소에 30%의 확률로 거짓말을 하는 사람이 있다고 해보겠습니다. 우리는 90%의 정확도를 가진 거짓말 탐지기를 통해 이 사람의 말이 거짓인지를 판단하고자 합니다.
이 문제는 거짓말 탐지기의 관찰결과를 토대로 어떤 사람의 말이 거짓일 사후확률 $P(A|B)$를 구하는 문제입니다.
이제 사후 확률 $P(A|B)$을 구하기 위해서 베이즈정리를 활용해보도록 하겠습니다.
먼저, 사전 확률 ${P(A)}$는 현재 저희가 알고 있는 정보에 의존합니다. 이 문제의 경우, 사전 확률 $P(A)$는 이 사람이 평소에 거짓말을 할 확률인 0.3입니다. likelihood $P(B|A)$ 역시 이미 알고 있다고 가정하는 경우가 많습니다.
이 문제의 경우, likelihood는 이 사람이 거짓말을 했을때 실제로 그것이 거짓이었을 확률 $P(B|A)$이므로 거짓말 탐지기의 정확도가 곧 likelihood입니다. 따라서 likelihood $P(B|A)$는 0.9(90%)입니다.
사전 확률 $P(B)$는 거짓말 탐지기가 거짓이라고 판정할 확률입니다. 따라서, $P(B)$는 거짓말인데 거짓이라고 판정한 경우 $P(B|A) *P(A)$와 거짓말이 아닌데 거짓이라고 판정한 경우 $P(B|A^c) *P(A^c)$의 합이 됩니다. 따라서 $P(B)$를 구하는 식은 아래와 같습니다.
P(B) = P(B|A) *P(A) + P(B|A^c) *P(A^c)
= 0.9 * 0.3 + 0.1 * 0.7
= 0.34
베이즈 정리 공식을 이용하여 구하고자하는 사후확률 $P(A|B)$은 \begin{align} P(A|B) = \frac{P(B|A)P(A)}{P(B)} = \frac {0.9 * 0.3}{0.34} = \frac {0.27}{0.34} = 0.794 \end{align}
계산결과 79.4%임을 알 수 있습니다. 거짓말 탐지기에 의해서 이 사람의 말이 거짓이라는 결과가 관찰되었고, 따라서 그 관찰된 결과에 따라서 이 사람이 거짓말할 확률이 79.4%로 갱신되었다는 것을 의미합니다.
Reference
https://angeloyeo.github.io/2020/01/09/Bayes_rule.html
https://needjarvis.tistory.com/620
http://solarisailab.com/archives/2614
https://blog.minitab.com/ko/adventures-in-statistics-2/understanding-analysis-of-variance-anova-and-the-f-test
https://brunch.co.kr/@jihoonleeh9l6/36
https://hyen4110.tistory.com/17